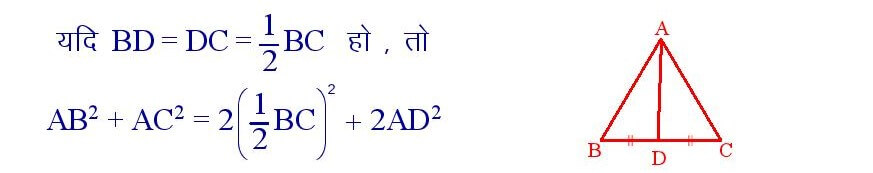सिद्धांत संख्या – 1
किसी त्रिभुज के तीनों कोणों का योग 1800 होता है।
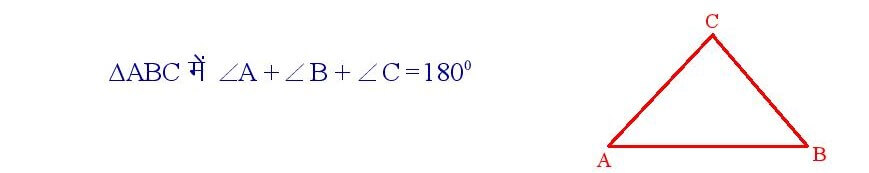सिद्धांत संख्या – 2
यदि किसी त्रिभुज की एक भुजा बढ़ाई जाए तो इस प्रकार बना बहिष्कोण दो अभिमुख अंतः कोणों के योग के बराबर होता है।
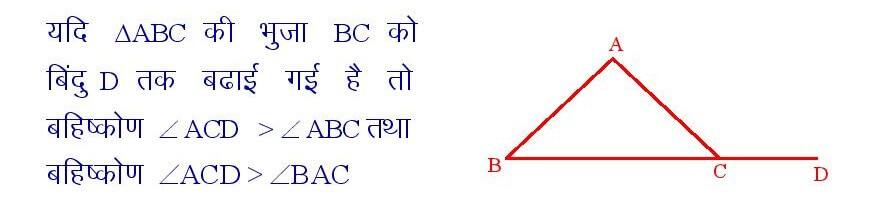
सिद्धांत संख्या – 3
किसी त्रिभुज का बहिष्कोण अभिमुख किसी एक अंतःकोण से हमेशा बड़ा होता है।
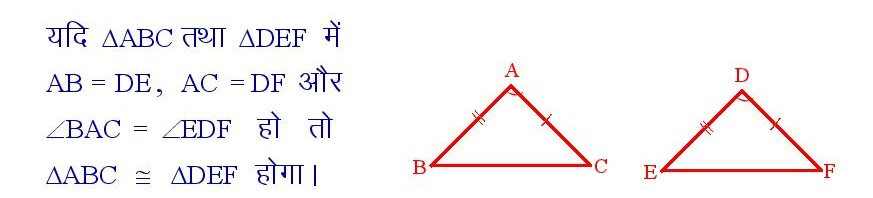
सिद्धांत संख्या – 4
यदि एक त्रिभुज की दो भुजाएं तथा उनके अंतर्गत कोण, दूसरे त्रिभुज की तदरूपी दोनों भुजाओं तथा उनके अंतर्गत कोण के बराबर हो, तो वे दोनों त्रिभुज सर्वांगसम होते हैं ।
इसे भुजा – कोण- भुजा या S – A – S अभिगृहीत कहते हैं।
सिद्धांत संख्या – 5
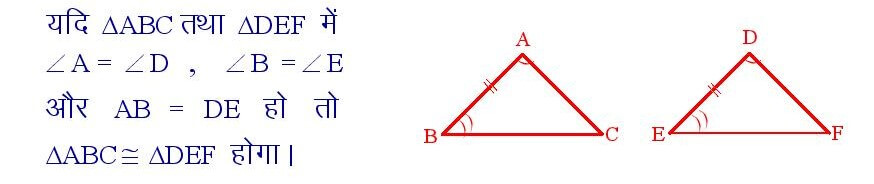
यदि किसी त्रिभुज के दो कोण तथा उनके बीच की भुजा , दूसरे त्रिभुज के तदनरूपी कोणों तथा उनके बीच की भुजा के बराबर हो , तो वे दोनों त्रिभुज आपस में सर्वांगसम होते हैं ।
इसे कोण – भुजा – कोण या A – S – A अभिगृहीत कहते हैं ।
सिद्धांत संख्या – 6
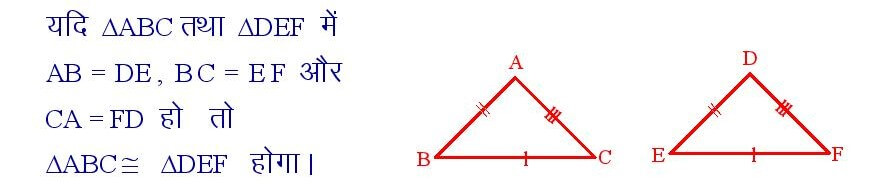
यदि किसी त्रिभुज के तीन भुजाएँ , दूसरे त्रिभुज के तदनरूपी भुजाओं के बराबर हो , तो वे दोनों त्रिभुज आपस में सर्वांगसम होते हैं ।
इसे भुजा – भुजा – भुजा या S – S – S अभिगृहीत कहते हैं ।
सिद्धांत संख्या – 7
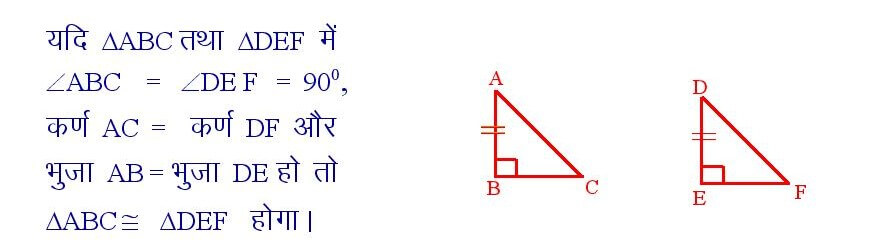
यदि किसी समकोण त्रिभुज के कर्ण और एक भुजा दूसरे समकोण त्रिभुज के तदनरूपी कर्ण और एक भुजा बराबर हो, तो वह दोनों त्रिभुज आपस में सर्वांगसम होते हैं।
इसे समकोण – कर्ण – भुजा या R – H – S अभिगृहीत कहते हैं ।
सिद्धांत संख्या – 8
किसी त्रिभुज के बराबर भुजाओं के सम्मुख कोण बराबर होते हैं ।
सिद्धांत संख्या – 9
किसी त्रिभुज में समान कोणो की सम्मुख भुजाएं समान होती है ।
सिद्धांत संख्या – 10
यदि किसी त्रिभुज की दो भुजाएं असमान हो , तो बड़ी भुजा के सामने का कोण , छोटी भुजा के सामने के कोण की अपेक्षा बड़ा होता है।
सिद्धांत संख्या – 11
किसी त्रिभुज में बड़ी भुजा के सामने का कोण बड़ा होता है।
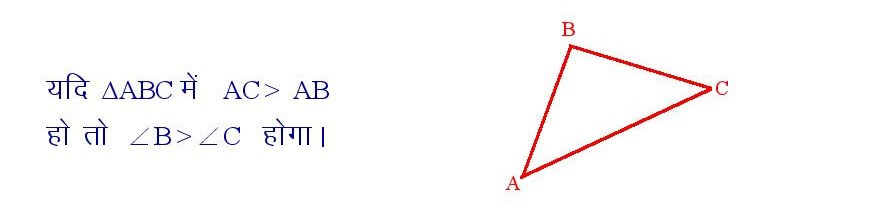
सिद्धांत संख्या – 12
किसी त्रिभुज की दो भुजाओं का योग तीसरी भुजा से बड़ा होता है ।
सिद्धांत संख्या – 13
किसी दी हुई रेखा के बाहर किसी बिंदु से उस रेखा पर जितने रेखाखंड खींचे जाते हैं उनमें लंब रेखाखंड सबसे छोटा होता है।
सिद्धांत संख्या – 14
किसी त्रिभुज में दो भुजाओं के मध्यबिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समानांतर तथा लंबाई में आधा होता है।
सिद्धांत संख्या – 15
किसी त्रिभुज के एक भुजा के मध्यबिंदु से किसी दूसरी भुजा के समानांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
सिद्धांत संख्या – 16
दो नियत बिंदुओं से समदूरस्थ किसी बिंदु का बिंदुपथ उन दो बिंदुओं को मिलाने वाली रेखाखंड का लंब समद्विभाजक होता है ।
सिद्धांत संख्या – 17
किसी त्रिभुज के कोणों के समद्विभाजन एक ही बिंदु से होकर जाती है।
सिद्धांत संख्या – 18
किसी त्रिभुज की भुजाओं के लंब समद्विभाजन एक ही बिंदु से होकर जाती है।
सिद्धांत संख्या – 19
किसी त्रिभुज की माध्यिकाएँ एक ही बिंदु से होकर जाती है और वह बिंदु प्रत्येक माधिका को 2 : 1 के अनुपात में बाँटती है।
सिद्धांत संख्या – 20
किसी त्रिभुज के तीनों शीर्षलंब एक ही बिंदु से होकर जाती है।
सिद्धांत संख्या – 21
यदि किसी समान क्षेत्रफल वाले त्रिभुज में , त्रिभुज की एक भुजा दूसरे त्रिभुज की एक भुजा के बराबर हो, तो उनके तदनरुपी शीर्ष- लंब समान होते हैं।
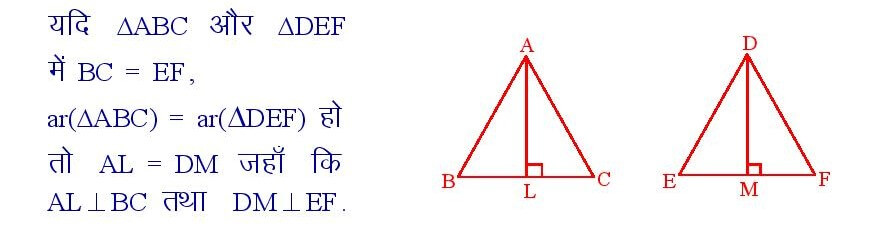
सिद्धांत संख्या – 22
किसी त्रिभुज का क्षेत्रफल उस त्रिभुज के एक भुजा तथा संगत शीर्षलंब के गुणनफल का आधा होता है।
सिद्धांत संख्या – 23
किसी त्रिभुज की कोई माधिका उसको दो बराबर क्षेत्रफल वाले त्रिभुजों में बाँटती है।
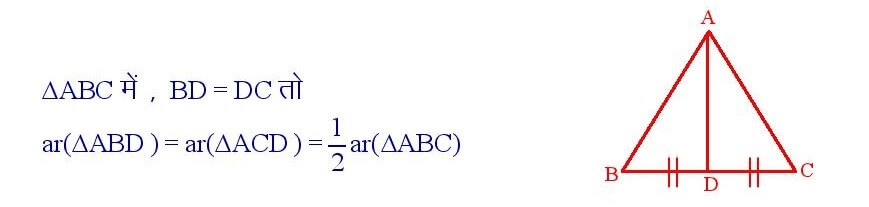
सिद्धांत संख्या – 24
यदि किसी त्रिभुज की किसी एक भुजा के समानांतर कोई रेखा खींची जाए तो अन्य दो भुजाओं को एक ही अनुपात में विभाजित करती है।
सिद्धांत संख्या – 25
यदि कोई रेखा किसी त्रिभुज की किन्ही दो भुजाओं को एक ही अनुपात में विभाजित करे तो वह रेखा तीसरी भुजा के समानांतर होती है।
सिद्धांत संख्या – 26
त्रिभुज के किसी कोण के आंतरिक या बाह्य समद्विभाजक उस कोण के बनाने वाली भुजाओं के अनुपात में सम्मुख भुजा को आंतरिकः या बाह्यतः विभाजित करता है।
सिद्धांत संख्या – 27
यदि किसी त्रिभुज का आधार आंतरिकतः या बाह्यतः ऐसे दो हिस्सों में बांटा जाए कि उसका अनुपात त्रिभुज की शेष दो भुजाओं के अनुपात के बराबर हो, तो विभाजन बिंदु तथा शीर्ष – बिंदु को मिलाने वाली सरल रेखा शीर्ष कोण को आंतरिक रूप या बाह्य रूप से समद्विभाजित करती है ।
सिद्धांत संख्या – 28
यदि किसी त्रिभुज के एक कोण के समद्विभाजक रेखा उसकी माध्यिका हो , तो वह त्रिभुज समद्विबाहु होगा।
सिद्धांत संख्या – 29
यदि किसी त्रिभुज की दो माध्यिकाएँ संबद्ध शीर्षकोण को समद्विभाजित करें तो वह त्रिभुज समबाहु होगा ।
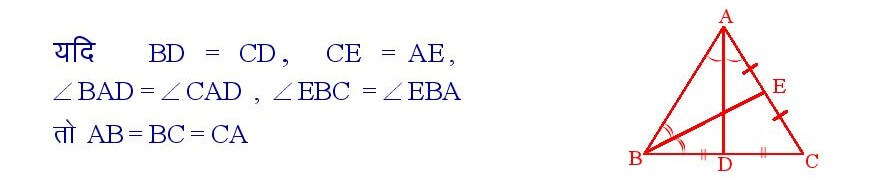
सिद्धांत संख्या – 30
यदि दो त्रिभुज ΔABC और ΔDEF समरूप हो , तो
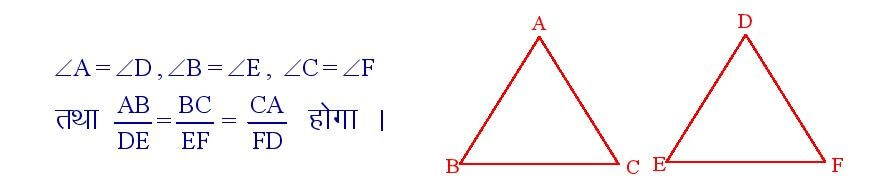
सिद्धांत संख्या – 31
यदि दो त्रिभुजों के संगत कोण बराबर हों , अर्थात दो त्रिभुज समकोणीक हों तो त्रिभुज समरूप होते हैं ।
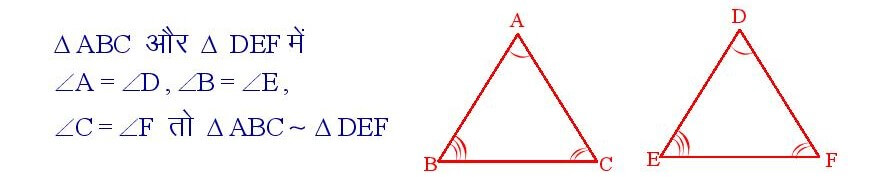
सिद्धांत संख्या – 32
यदि एक त्रिभुज के दो कोण , दूसरे त्रिभुज के दो कोणों क्रमशः बराबर हो , तो वे दोनों त्रिभुज समरूप होंगे।
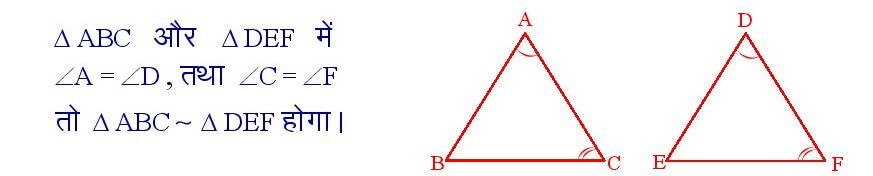
सिद्धांत संख्या – 33
यदि दो त्रिभुजों की संगत भुजाएं अनुपातिक हो , तो वे त्रिभुज समरूप होते हैं।
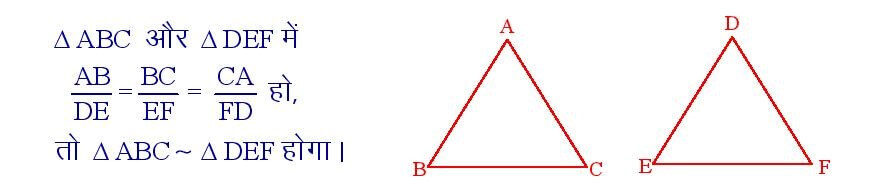
सिद्धांत संख्या – 34
यदि दो त्रिभुजों में संगत भुजाओं का एक युग्म आनुपातिक हो और आंतरिक कोण बराबर हों तो वह दोनों त्रिभुज समरूप होंगे ।
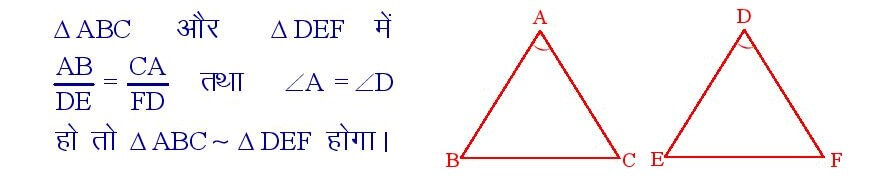
सिद्धांत संख्या – 35
किसी समकोण त्रिभुज में समकोण बनाने वाले शीर्ष से कर्ण पर डाला गया लंब रेखा के दोनों ओर के त्रिभुज परस्पर और मूल त्रिभुज के समरूप होते हैं । साथी ही लंब का वर्ग कर्ण के दो भागों की लंबाइयों के गुणनफल के बराबर होते हैं।
सिद्धांत संख्या – 36
किसी दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।
सिद्धांत संख्या – 37
यदि दो त्रिभुज समकोणिक हो , तो संगत भुजाओं का अनुपात वही होता है जो संगत माध्यिकाएँ , कोणों के समद्विभाजक खंडों तथा शीर्ष – लंबों का होता है।
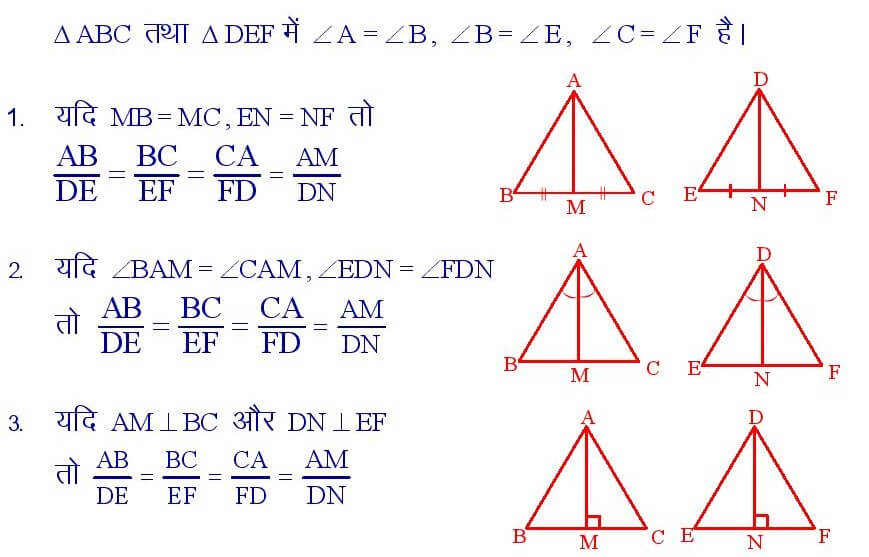
सिद्धांत संख्या – 38
दो समरूप त्रिभुजों के क्षेत्रफल संगत शीर्ष – लंबों , माध्यिकाओं तथा कोण – समद्विभाजकों के वर्गों के अनुपात के बराबर होता है।
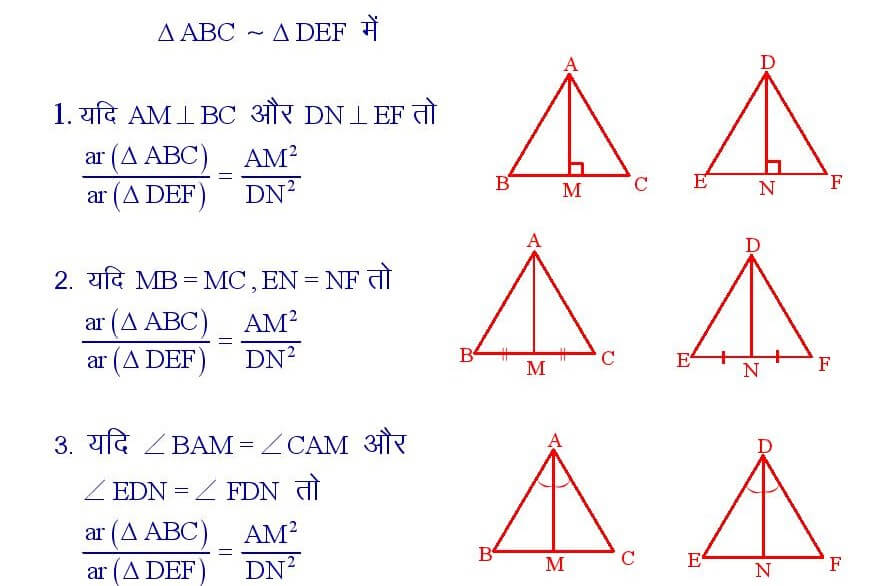
सिद्धांत संख्या – 39
दो समरूप त्रिभुजों के परिमापों का अनुपात उनके संगत भुजाओं के अनुपात के बराबर होता है।
सिद्धांत संख्या – 40
एक समकोण त्रिभुज में कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है।
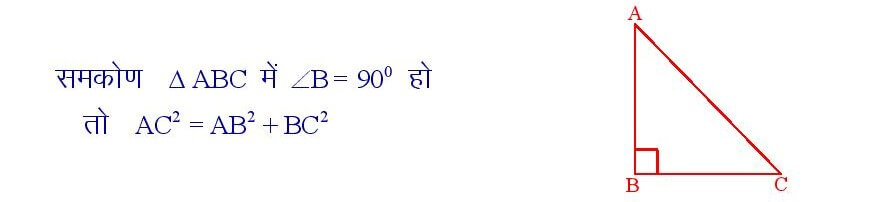
सिद्धांत संख्या – 41
यदि किसी त्रिभुज की किसी एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा के सामने का कोण समकोण होता है।
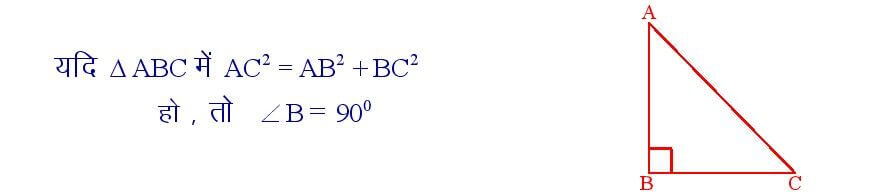सिद्धांत संख्या – 42
यदि ΔABC का कोण ∠B अधिककोण हो और AD भुजा CB के बढ़ाए हुए भाग पर लंब हो तो AB , BC , AC और BD में एक संबंध होता है ।
सिद्धांत संख्या – 43
यदि ΔABC का कोण ∠B न्यूनकोण हो और AD भुजा BC पर लंब हो तो AB , BC , AC और BD में एक संबंध होता है।
सिद्धांत संख्या – 44
किसी त्रिभुज में दो भुजाओं के वर्गों का योग बराबर होता है तीसरी भुजा के आधे के वर्ग के दुगुने और तीसरी भुजा की माध्यिका के वर्ग के दुगुने के योग के
