Triangles For 9th Class
1. Triangle : A plane figure bounded by three line segments is called a triangle.

2. Types of Triangle :
Types of triangle on the Basis of sides.
(i). Equilateral Triangle : A triangle having all sides equal is called an equilateral triangle.

(ii). Isosceles Triangle : A triangle having two sides equal is called an isosceles triangle.
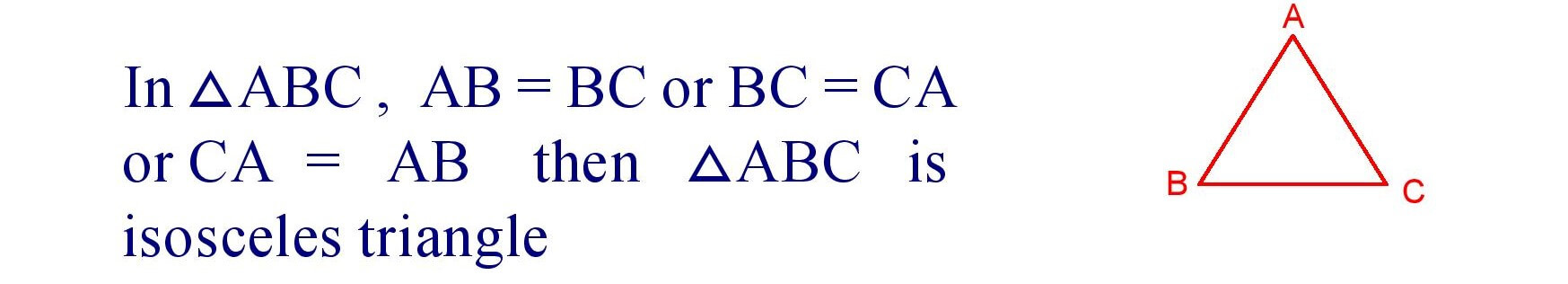
(iii). Scalene Triangle : A triangle in which all the sides are of different length is called a scalene triangle.
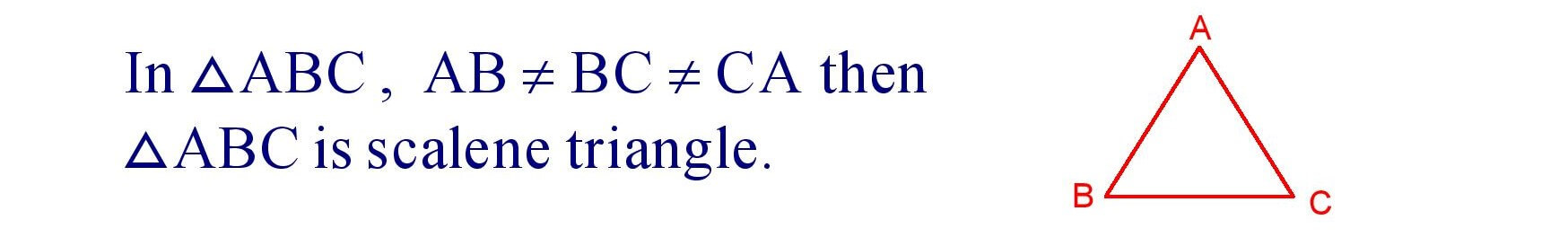
Types of triangles on the Basis of angles.
(iv). Right Angled Triangle : A triangle in which one of the angles measures 900 is called a right – angled triangle.
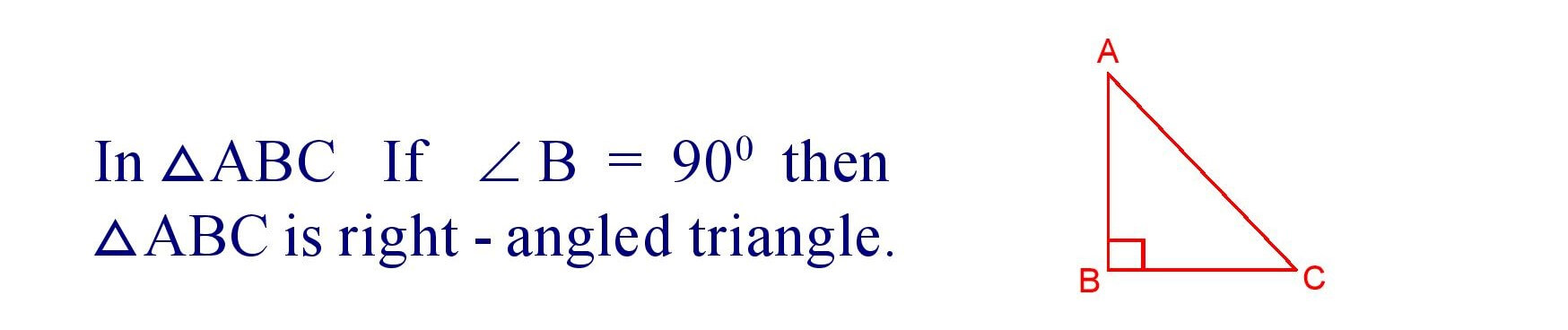
(v). Acute – Angled Triangle : A triangle in which every angle measures more than 00 and less than 900 is called an acute – angled triangle.
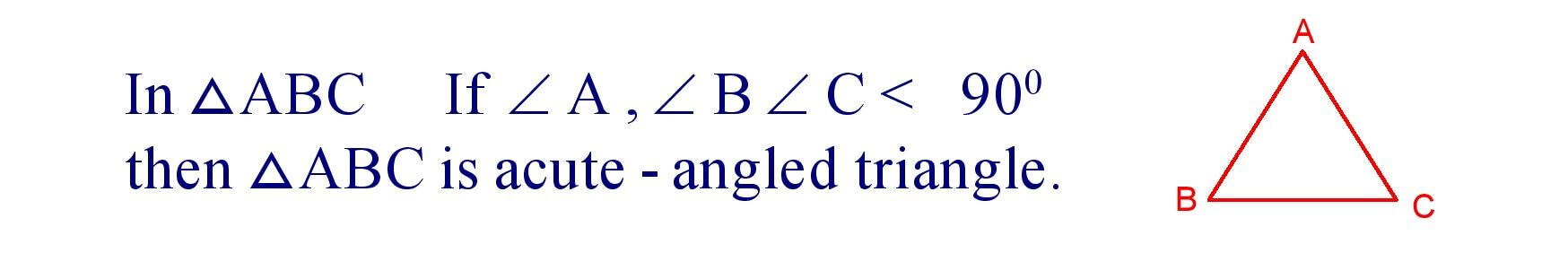
(vi). Obtuse – Angled Triangle : A triangle in which one of the angles measures more than 900 and less then 1800 is called an obtuse – angled triangle.
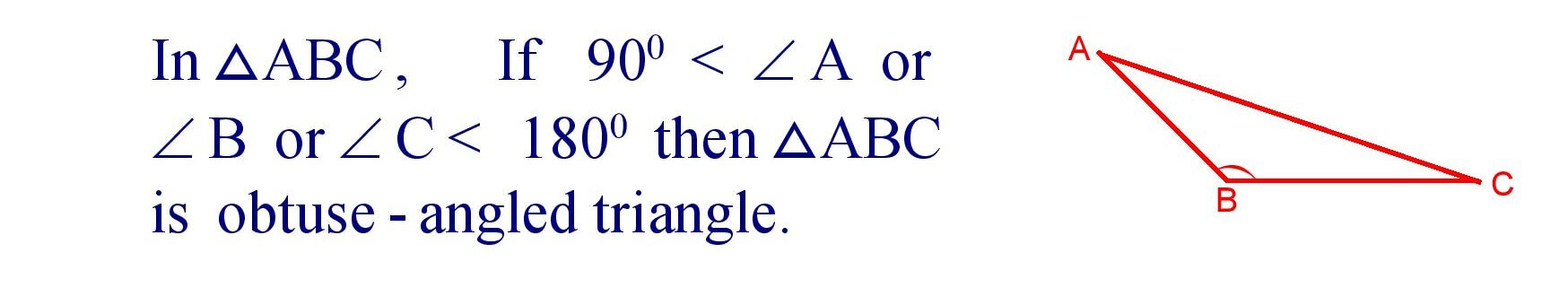
3. Medians of Triangle : The median of a triangle corresponding to any side is the line segment joining the midpoint of that side with the opposite vertex.

4. Centroid of Triangle : The point of intersection of all the three medians of a triangle is called its centroid.

5. Altitudes of Triangle : The altitude of a triangle corresponding to any side is the length of perpendicular drawn from the opposite vertex to that side.

6. Orthocentre of Triangle : The point of intersection of all the three altitudes of a triangle is called its orthocentre.

7. Incentre of Triangle : The point of intersection of the internal bisectors of the angles of a triangle ia called its incentre.

8. Circumcentre of Triangle : The point of intersection of the perpendicular bisectors of the sides of a triangle is called its cicumcentre.

9. Some Properties of Triangle.
(a). Sum of three angles of triangle is 1800

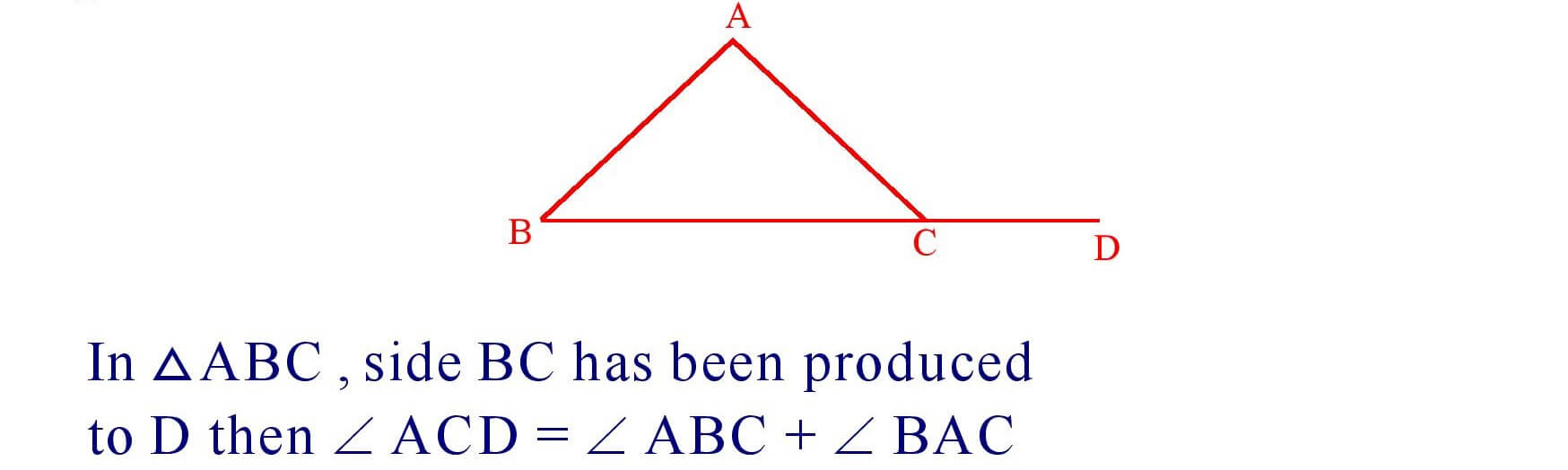
(b). If a side of a triangle is produced then the exterior angle so formed is equal to the sum of two interior opposite angles.
(c). An exterior angle of a triangle is greater than either of the interior opposite angles.
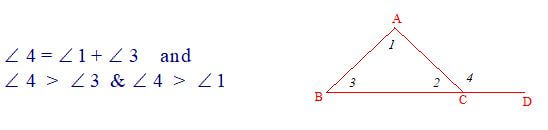
| Click here to pdf download |