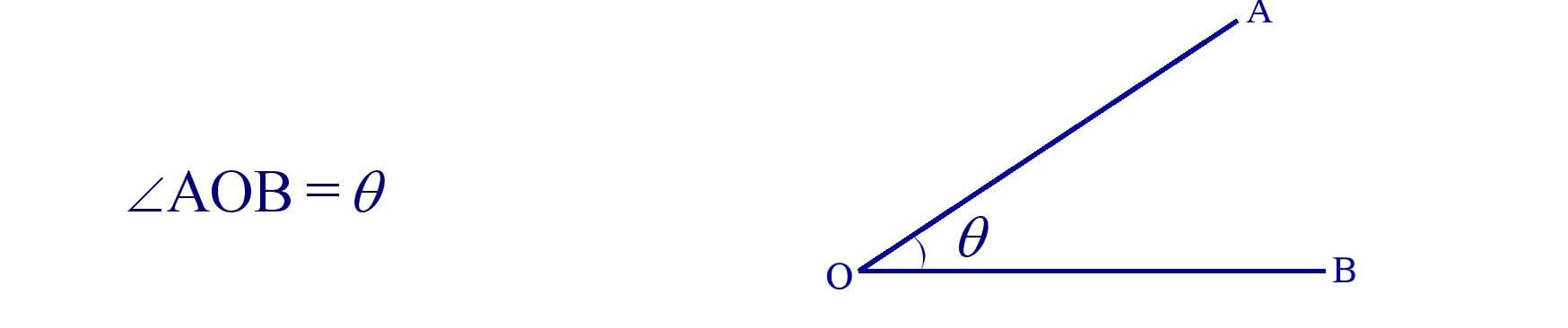
1. Angle : Two ray OA and OB having a common end point O from ∠AOB.
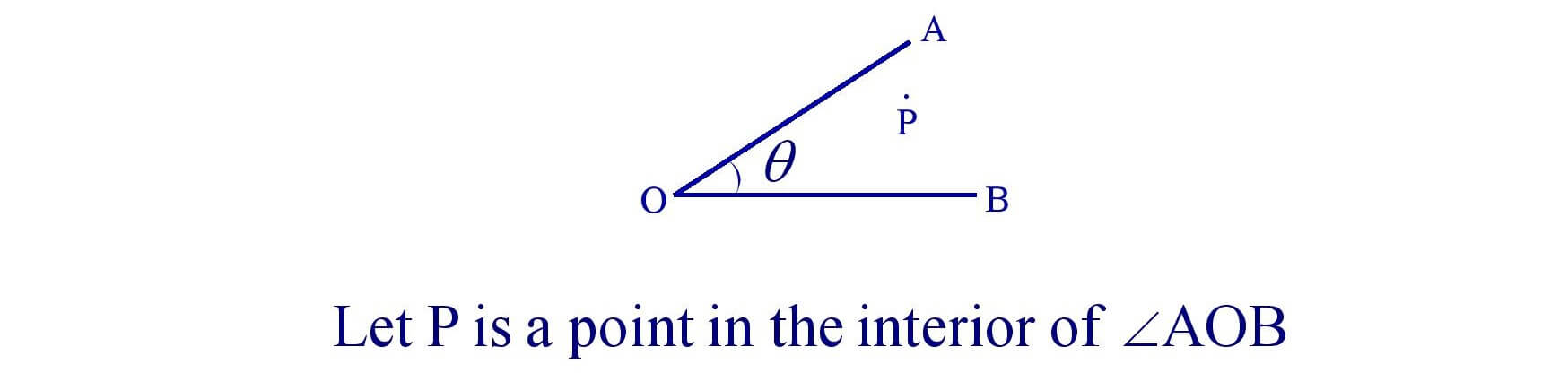
2. Interior of an Angle : The interior of an angle ∠AOB is the set of all points in its plane, which lie on the same side of OA as B and also on the same side of OB as A.
3. Exterior of an Angle : The exterior of an angle ∠AOB is the set of all those points in its plane , which do not lie on the angle or in its interior.

4. An angle of 3600 : If a ray OA starting from its original position OA , rotates about O in the anticlockwise direction and after making a complete revolution it come back to its original position.

5. Types of Angle :
(i). Right Angle : An angle whose measure 900 is called a right angle.

(ii). Acute Angle : An angle whose measure is more than 00 but less than 900 is called an acute angle.

(iii). Obtuse Angle : An angle whose measure is more than 900 but less than 1800 is called an obtuse angle.

(iv). Straight Angle : An angle whose measure 1800 is called a straight angle.

(v). Reflex Angle : An angle whose measure is more than 1800 but less than 3600 is called reflex angle.

(vi). Complete Angle : An angle whose measure 3600 is called a complete angle.

6. Equal Angles : Two angles are said to be equal , if they have the same measure.
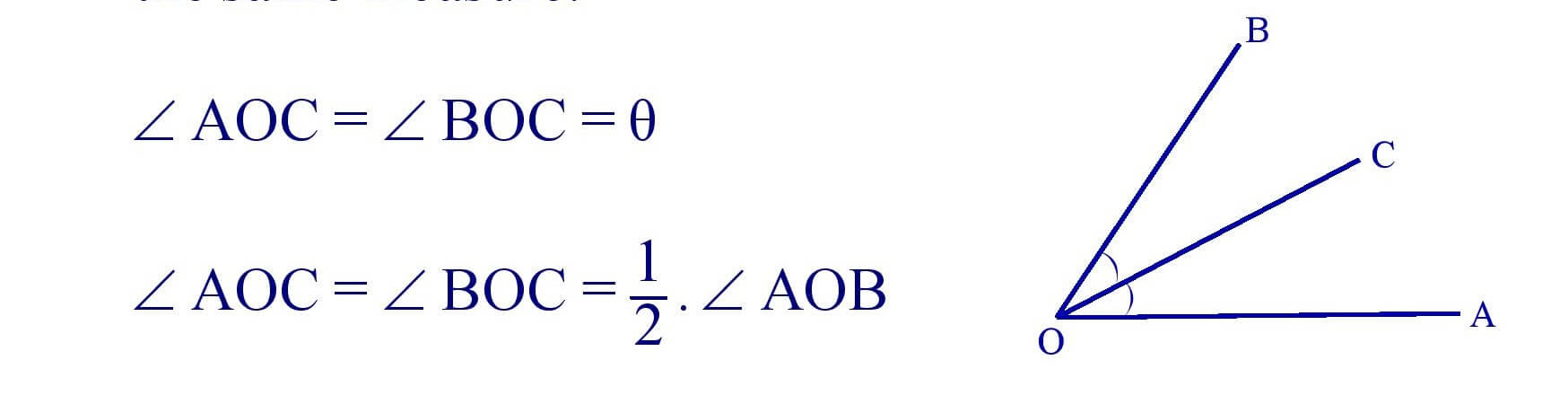
7. Complementary Angle : Two angle are said to be complementary , if the sum of their measures is 900.

8. Supplementary Angle : Two angle are said to be supplementary , if the sum of their measures is 1800.
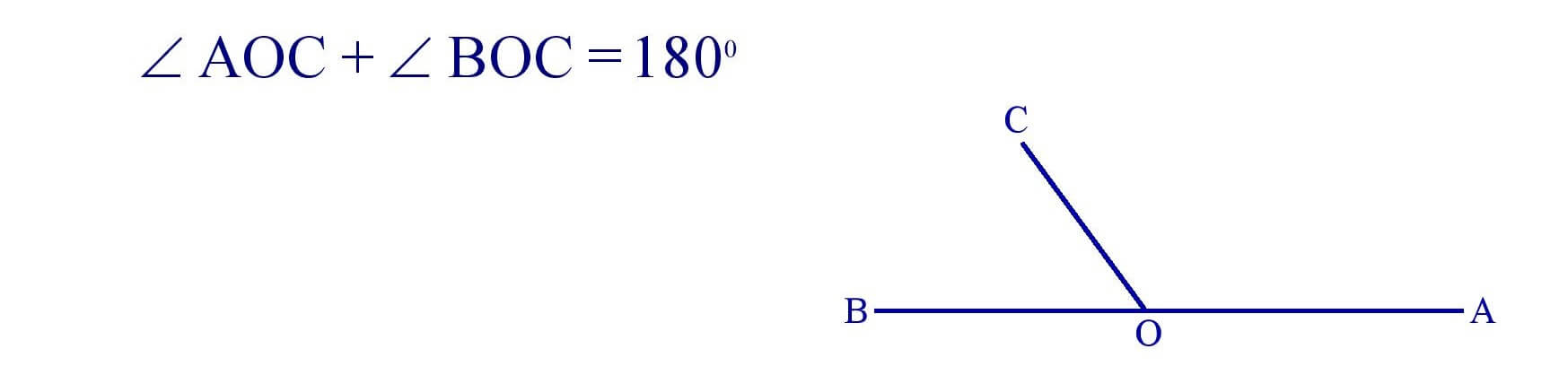
9. Adjacent Angles : Two angles are called adjacent angles if –

10. Some Results on Angle Relations.
(i). If a ray stands on a line then the sum of the adjacent angles is 1800.

(ii). The sum of all the angles fromed on the same side of a line at a point on the line is 1800.
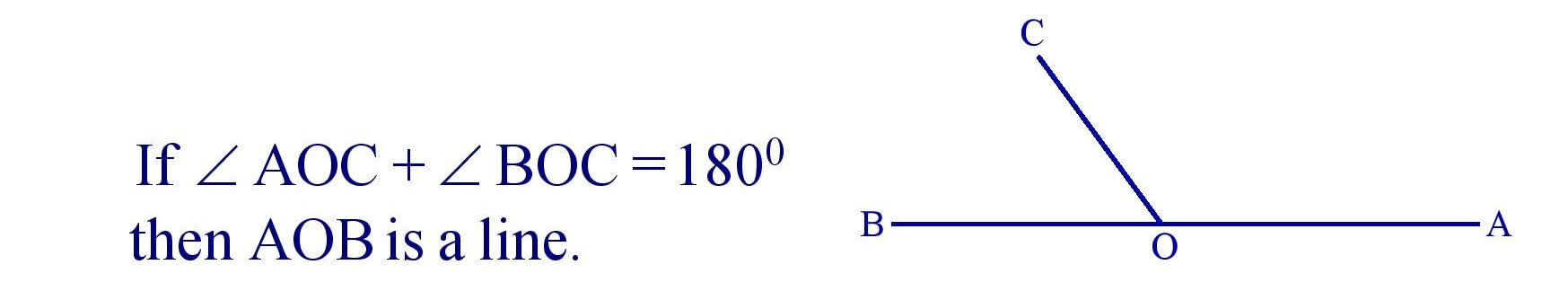
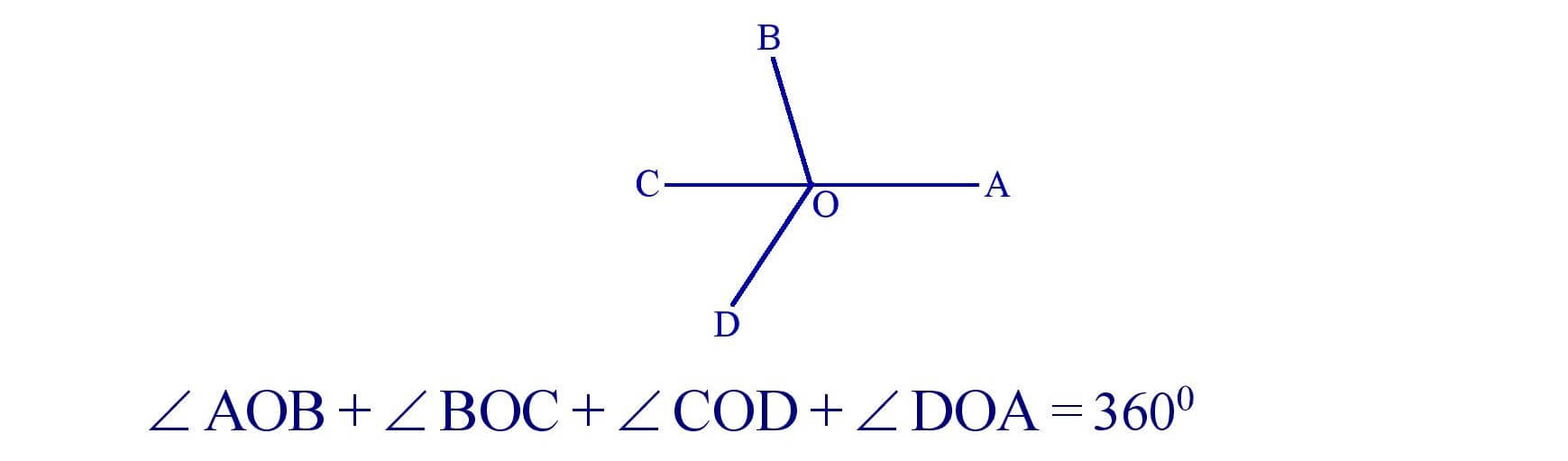
(iii). The sum of all the angles around a point is 3600
(iv). If the sum of two adjacent angles is 1800 then the non – common arms of the angles are in a straight line.

(v). Two angles are called a pair of vertically opposite angles , if their arms form two pairs of opposite rays.

(vi). If two lines intersect then the vertically opposite angles are equal.

11. Parallel Lines : If two lines lie in the same plane and do not intersect when produced on either side then such lines are said to be parallel to each other.

12. If a transversal cuts two parallel lines then each pair of corresponding angles are equal.
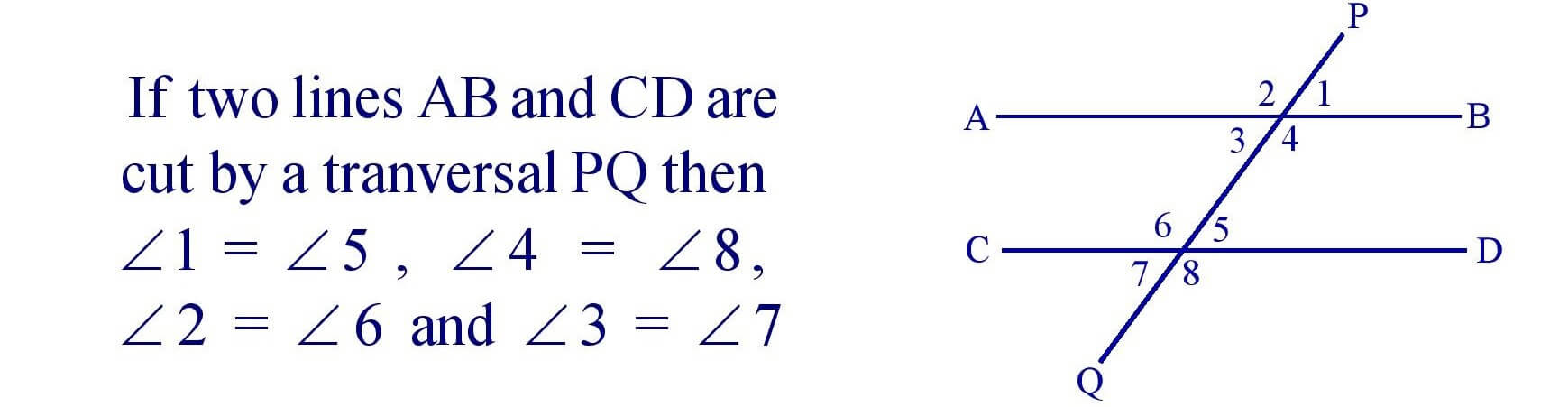
13. If a transversal intersects two parallel lines then alternate angles of each pair of interior angles are equal.

14. If a transversal intersects two parallel lines then each pair of consecutive interior angles are supplementary.

15. If a transversal intersects two lines making a pair of alternate interior angles equal, then the two lines are parallel.

16. If a transversal intersects two lines in such a way that a pair of consecutive interior angles are supplementary then the two lines are parallel.

| Click here to pdf download |
