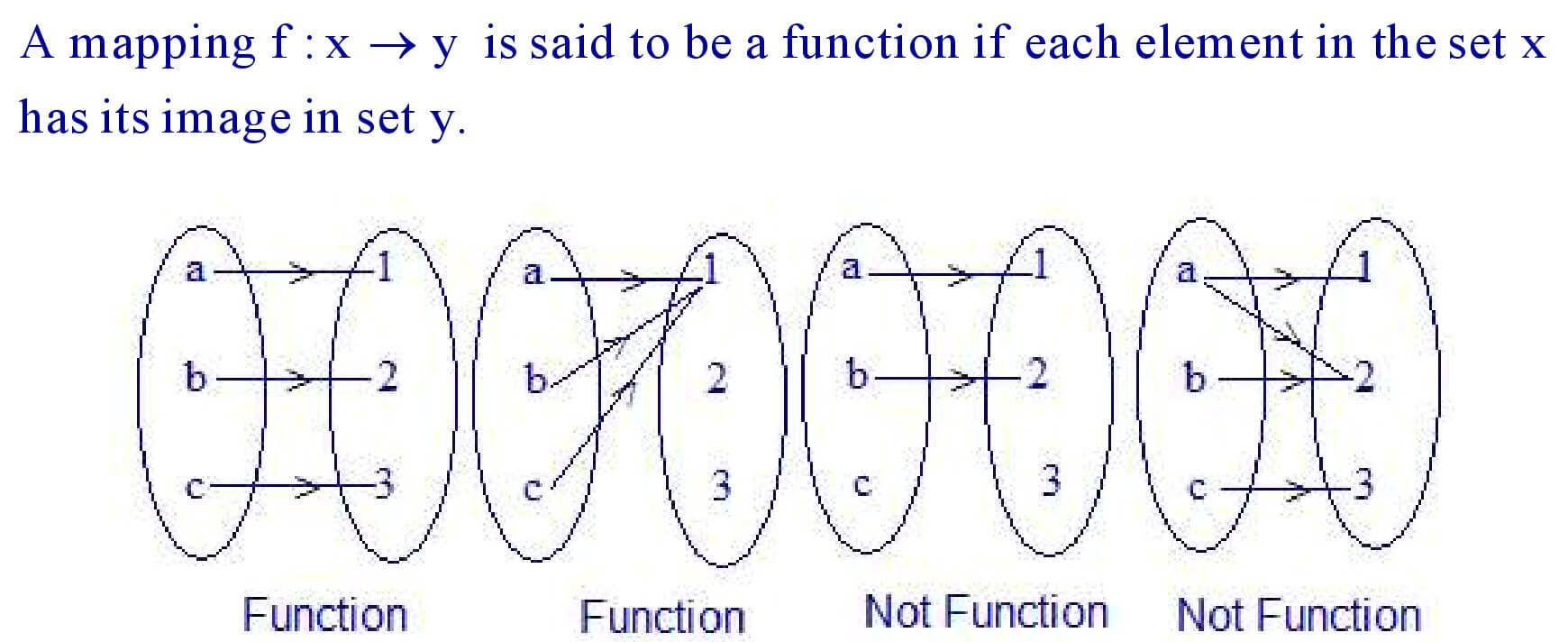
1. Definition of function :
2. Domain , Co – Domain and Range of a Function :

3. Formula for the Domain of a function.

4. Working Rule to find the Domain and Range of a Function.

Example :

5. Types of Function:
5.1 Mapping of Function :
(i). One – One function (Injective function) :

(ii). Many – One function :

(iii). Into function :

(iv). Onto – function ( Surjective Function ) :

5.2 Algebraic Functions : – These are the functions consisting of finite number of terms involving power and radicals of the independent variable , constants and fundamental mathematical operations (+) , (-) , (÷) (×)
(i). Polynomial Functions :
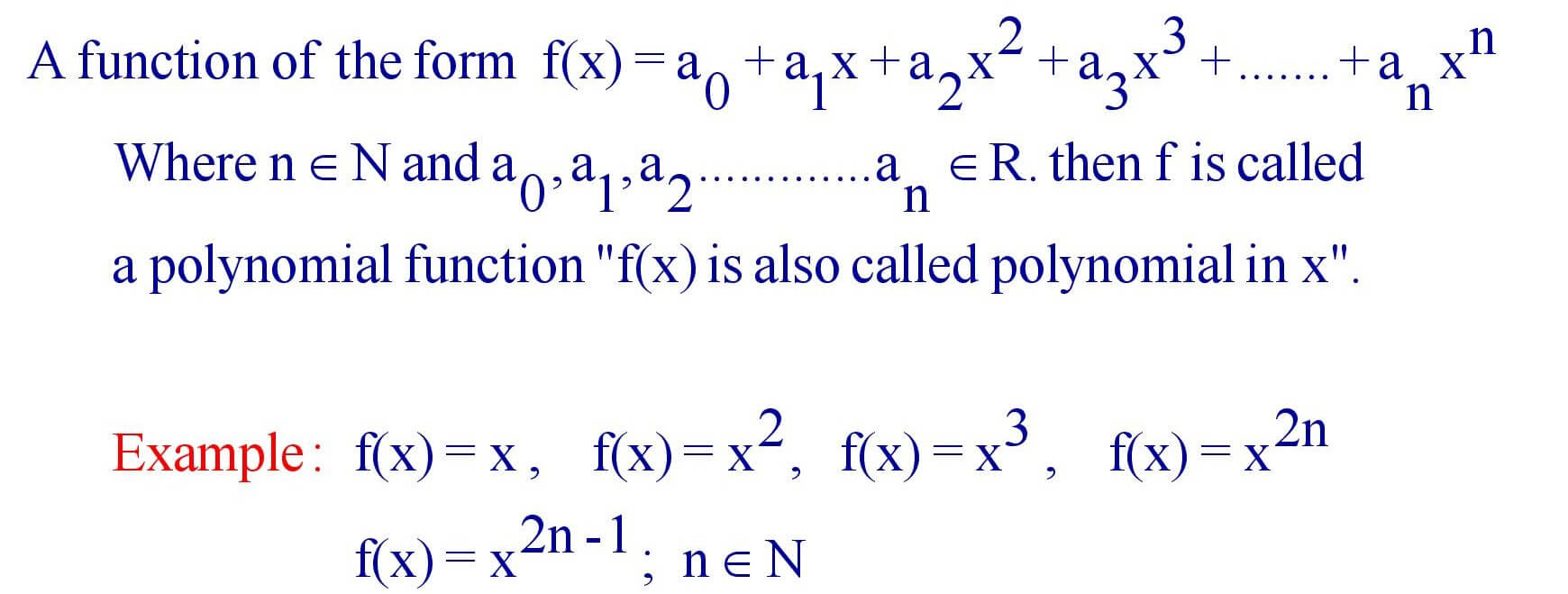
(ii). Fractional Rational Functions :

(iii). Irrational Function :

5.3 Transcendental Function : The functions which are not algebraic are called transcendental function.
(i). Exponential
(ii). Logarithmic
(iii). Trigonometric
(iv). Inverse trigonometric functions are transcendental functions.
(i). Exponential Function :
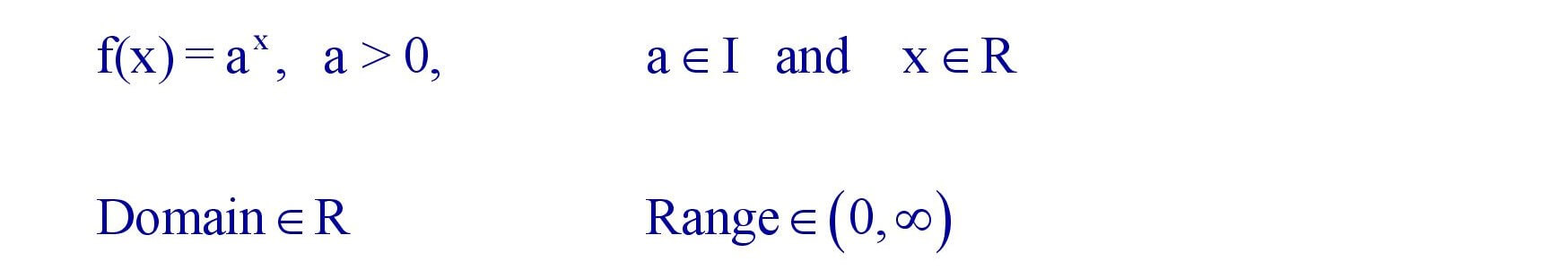
Case (a) : –

Case (b) :

(ii). Logarithmic Function :
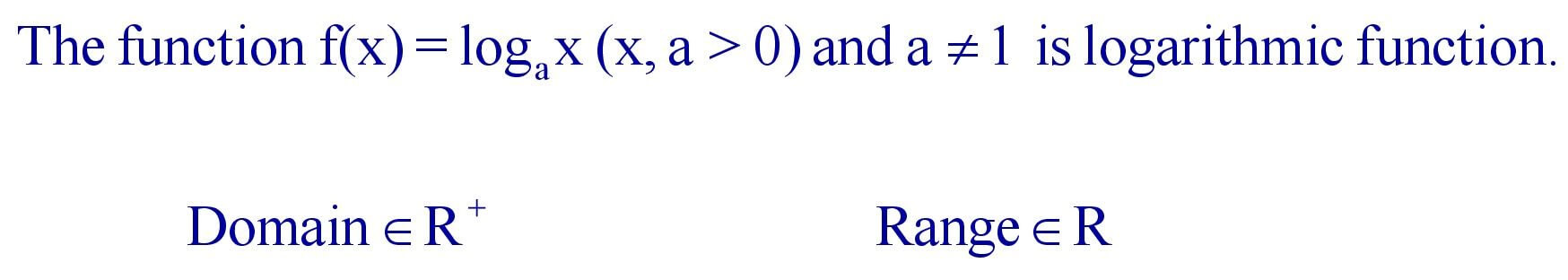
Note :
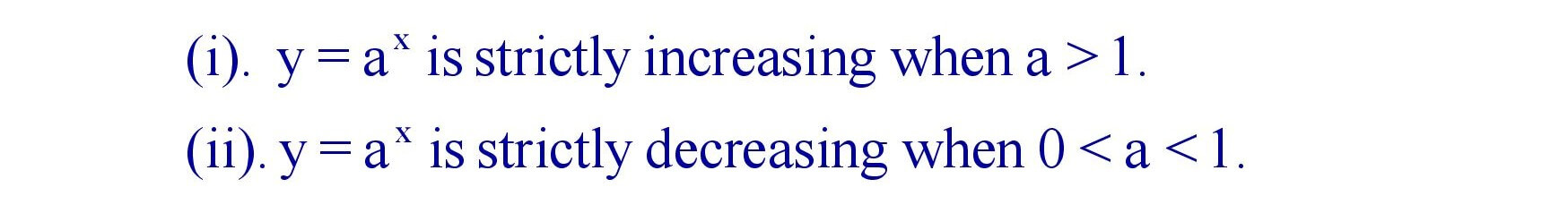
Properties of logarithmic Function :

(iii). Trigonometric Function :
(a). Sine Function : – F(x) = Sinx

(b). Cosine Function : F(x) = Cosx

(c). Tangent Function : F(x) = Tanx
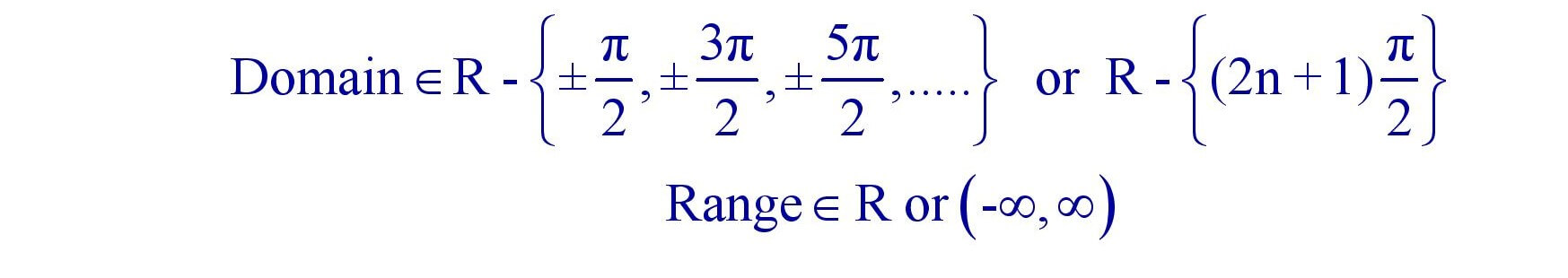
(d). Cosecant Function : f(x) = Cosecx is periodic with period 2π.
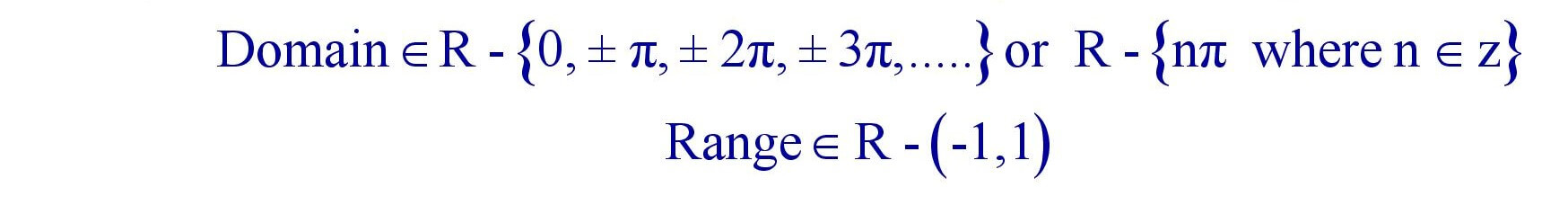
(e). Secant Function : f(x) = Secx is periodic with period 2π.
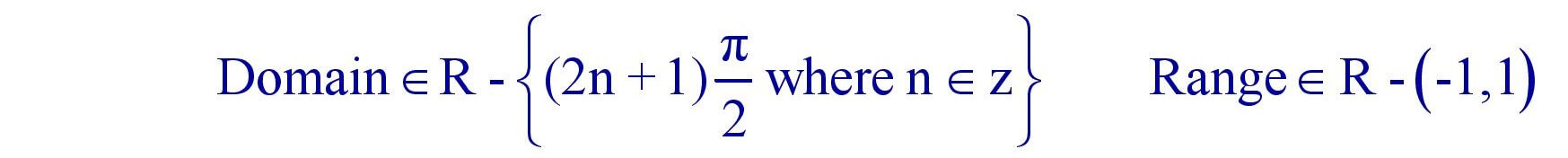
(f). Cotangent Function : F(x) = Cotx is periodic with period π.

(iv). Inverse Trigonometric Curves :



5.4 Piecewise Function : As discussed piscussed picewise function are :
(i). Absolute value function (or modulus Function )
(ii). Signum Function
(iii). Greatest interger function
(iv). Fractional part function
(v). Least interger function.
(i). Absolute value function (or modulus Function ) :
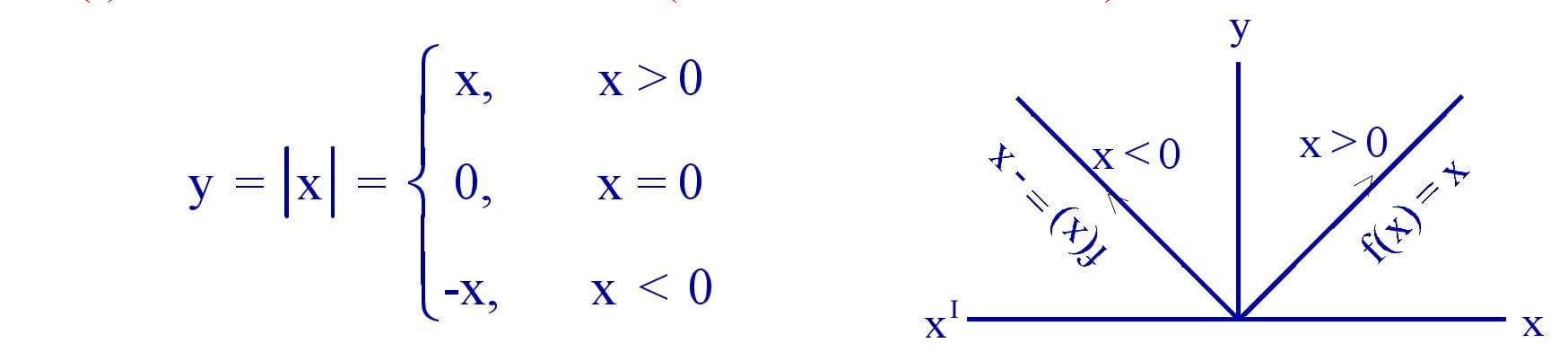
Properties of modulus function.

(ii). Signum Function : y = Sgn(x)
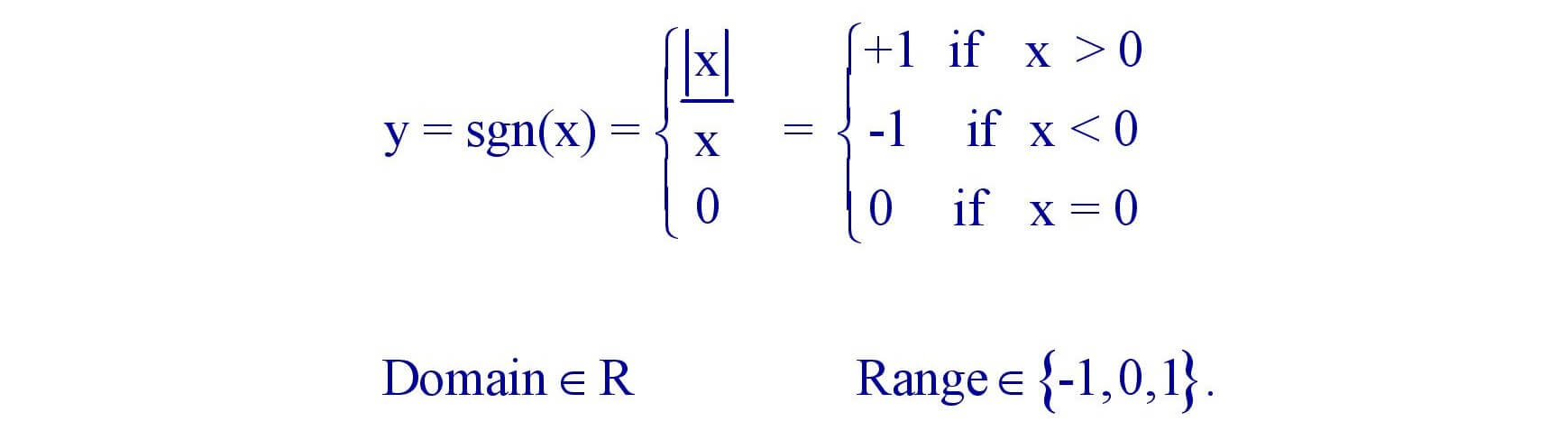
(iii). Greatest interger function :

Properties of greatest integer function :
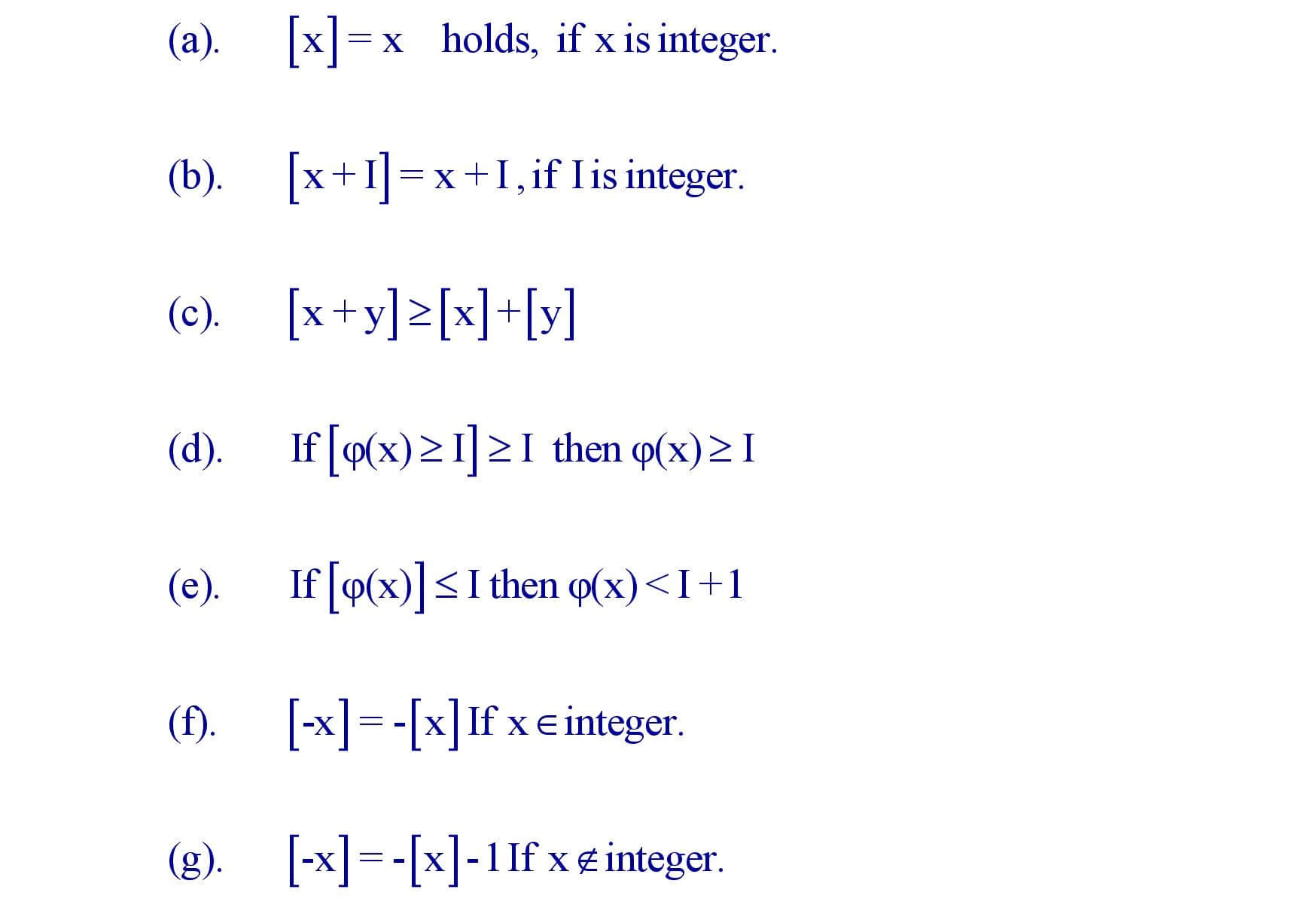
(iv). Fractional part function :

Properties of fractional part of x.
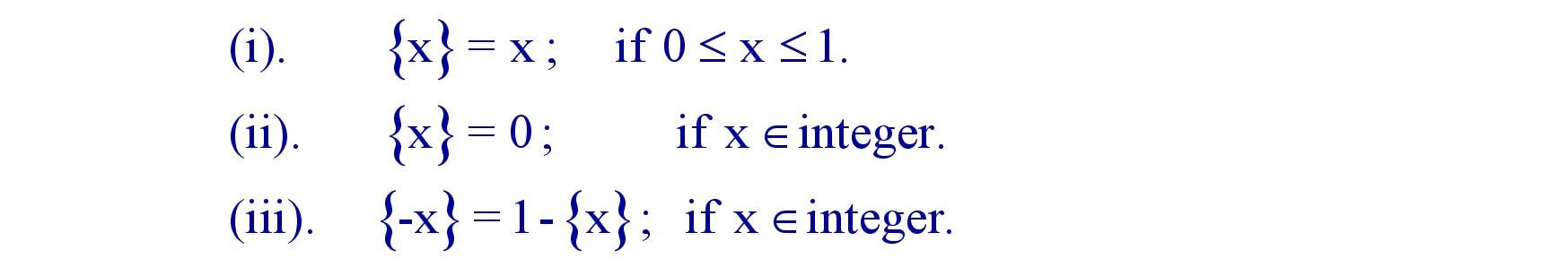
(v). Least interger function :

Properties of fractional part of x.
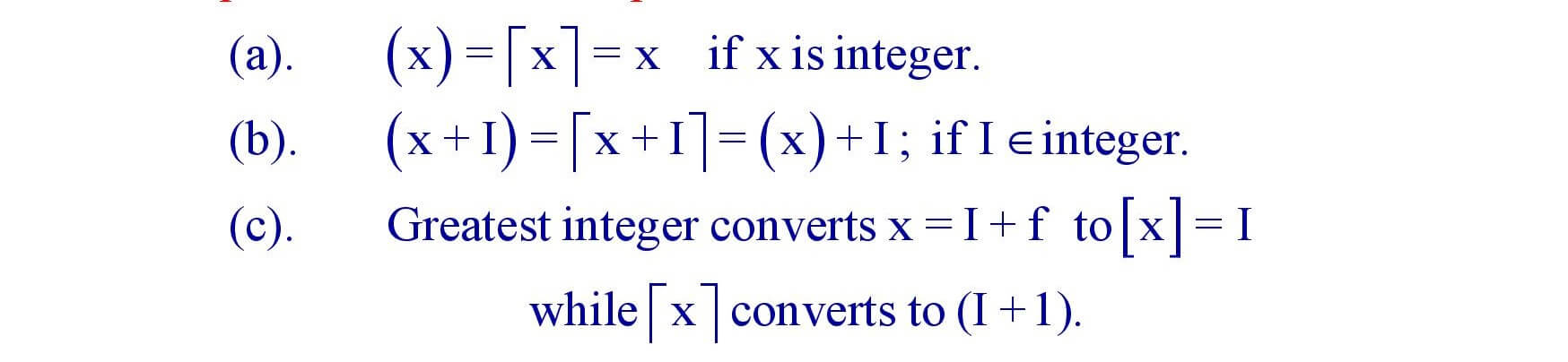
5.5 Constant function :
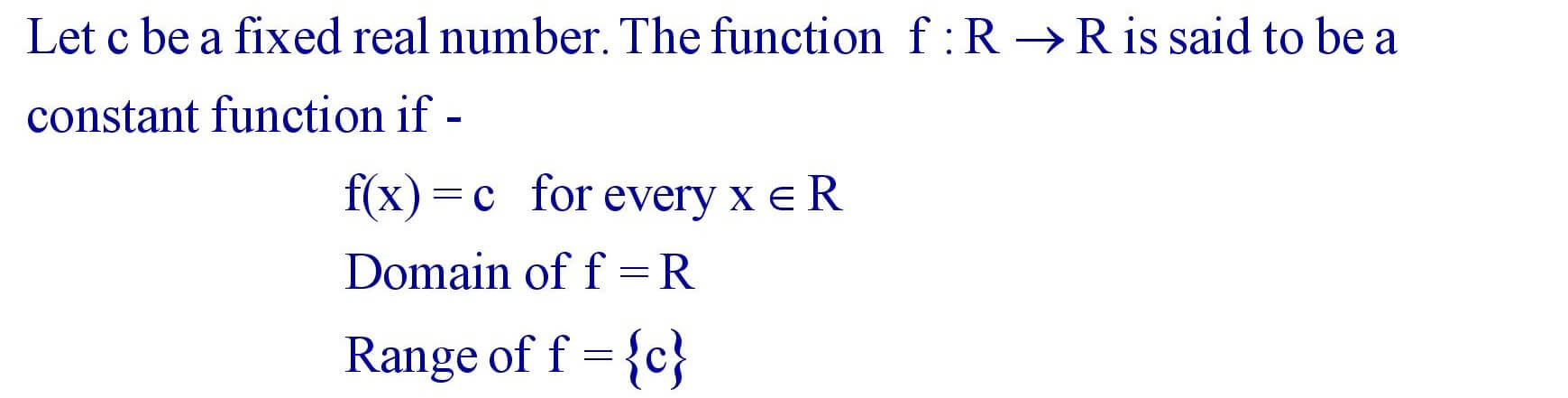
5.6 Principal square root function :

5.7 Equal or Identical Function :

5.8 Odd Function :
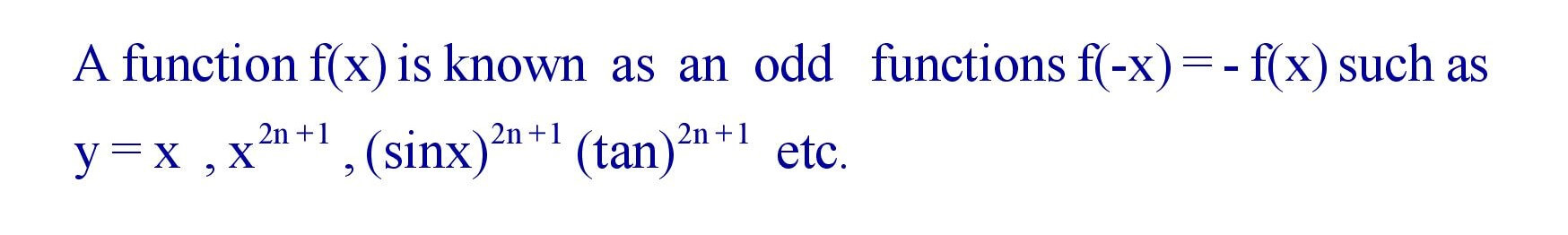
5.9 Even Function :
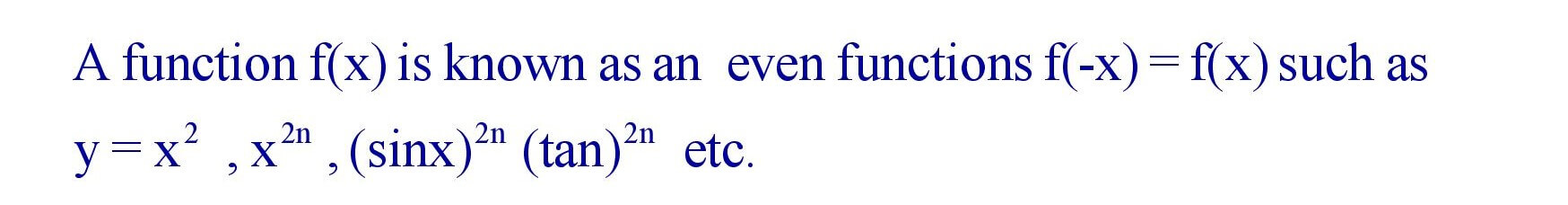
5.10 Geometrical Curves :
(i). Straight line :
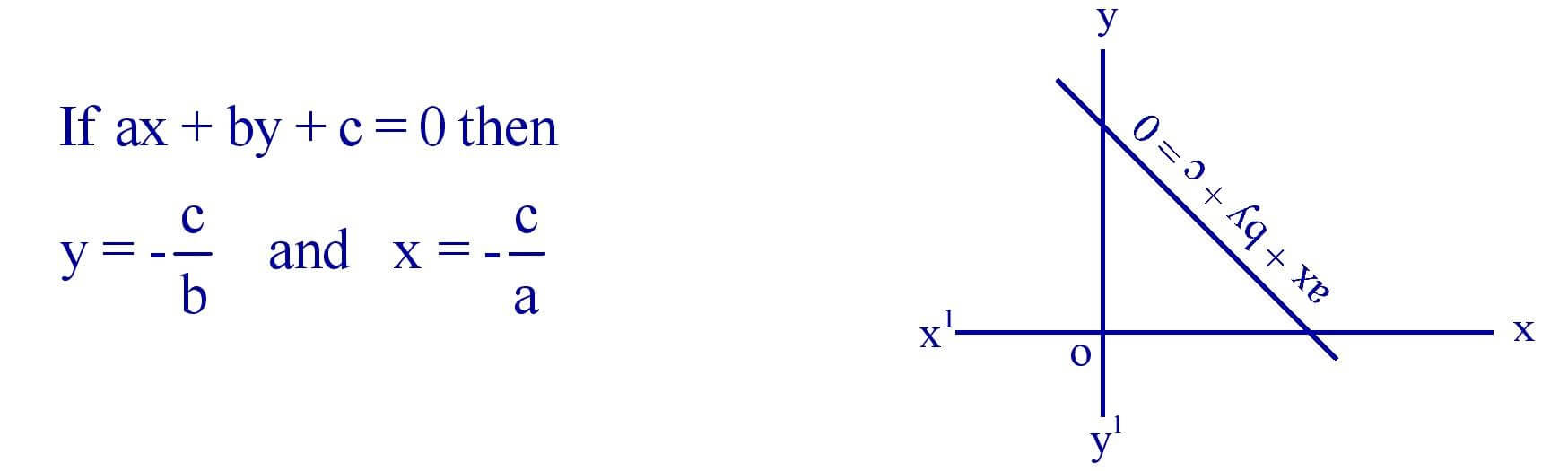
(ii). Quadratic Equations :
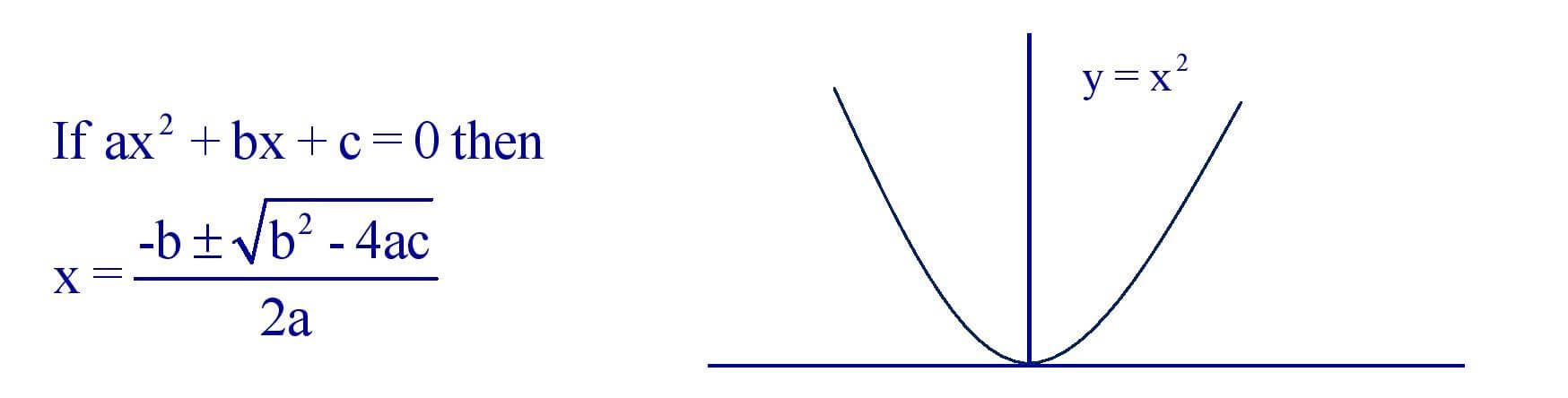
(iii). Circle :
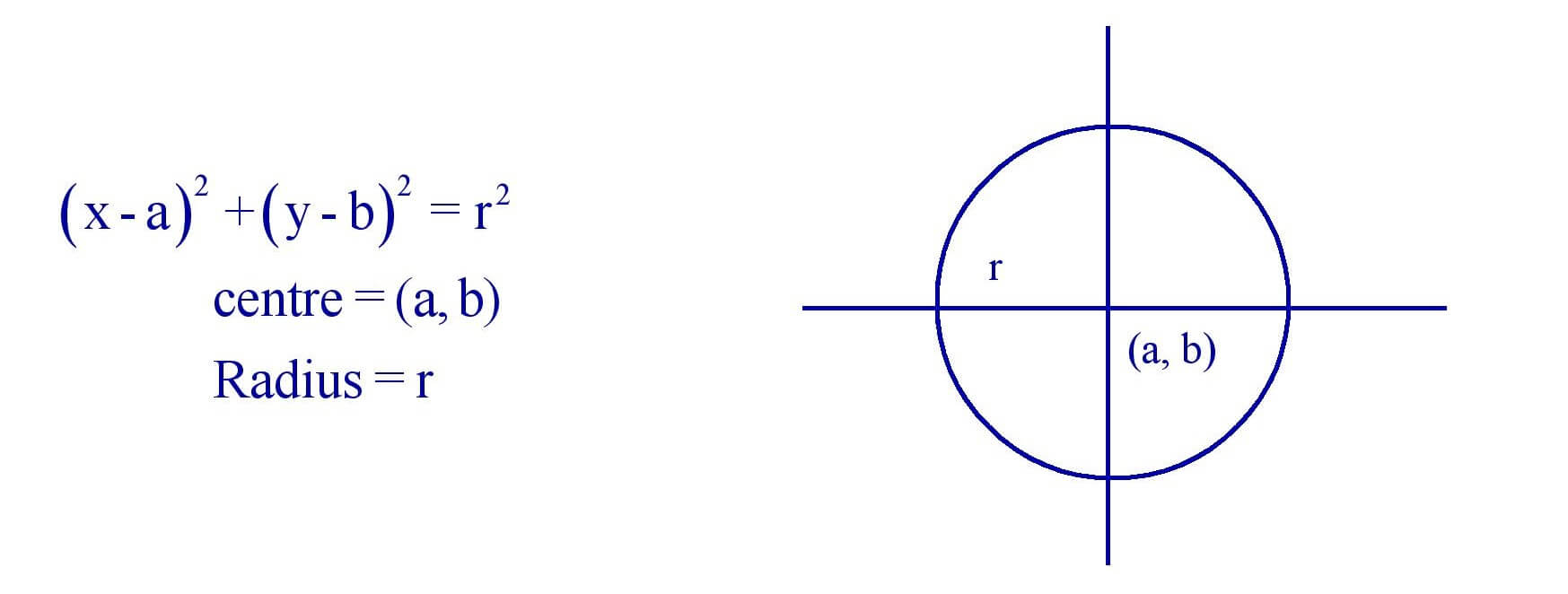
(iv). Parabola :
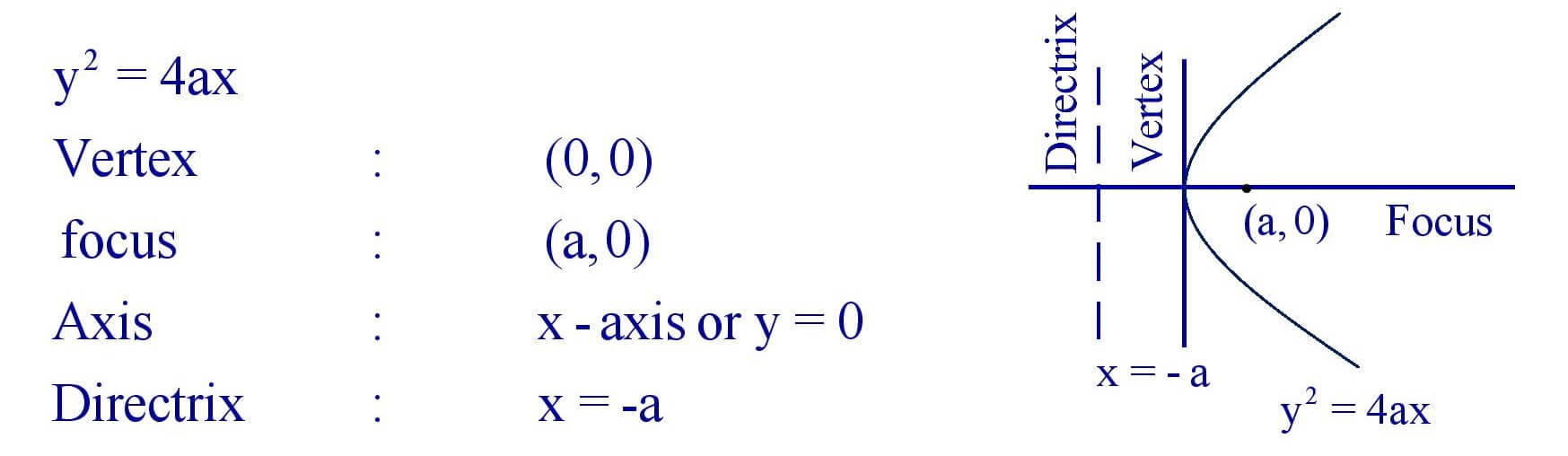
(v). Hyperbola :
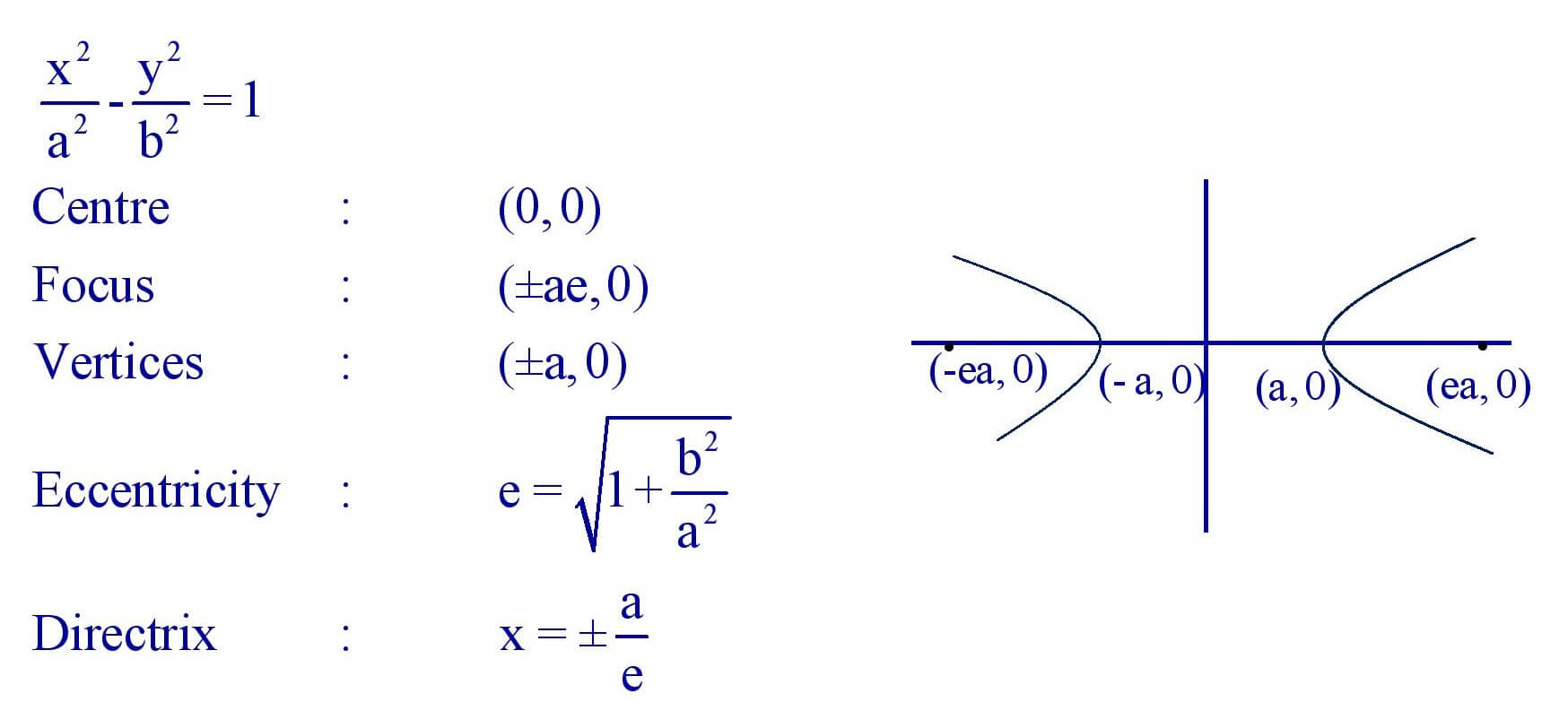
(vi). Ellipse :
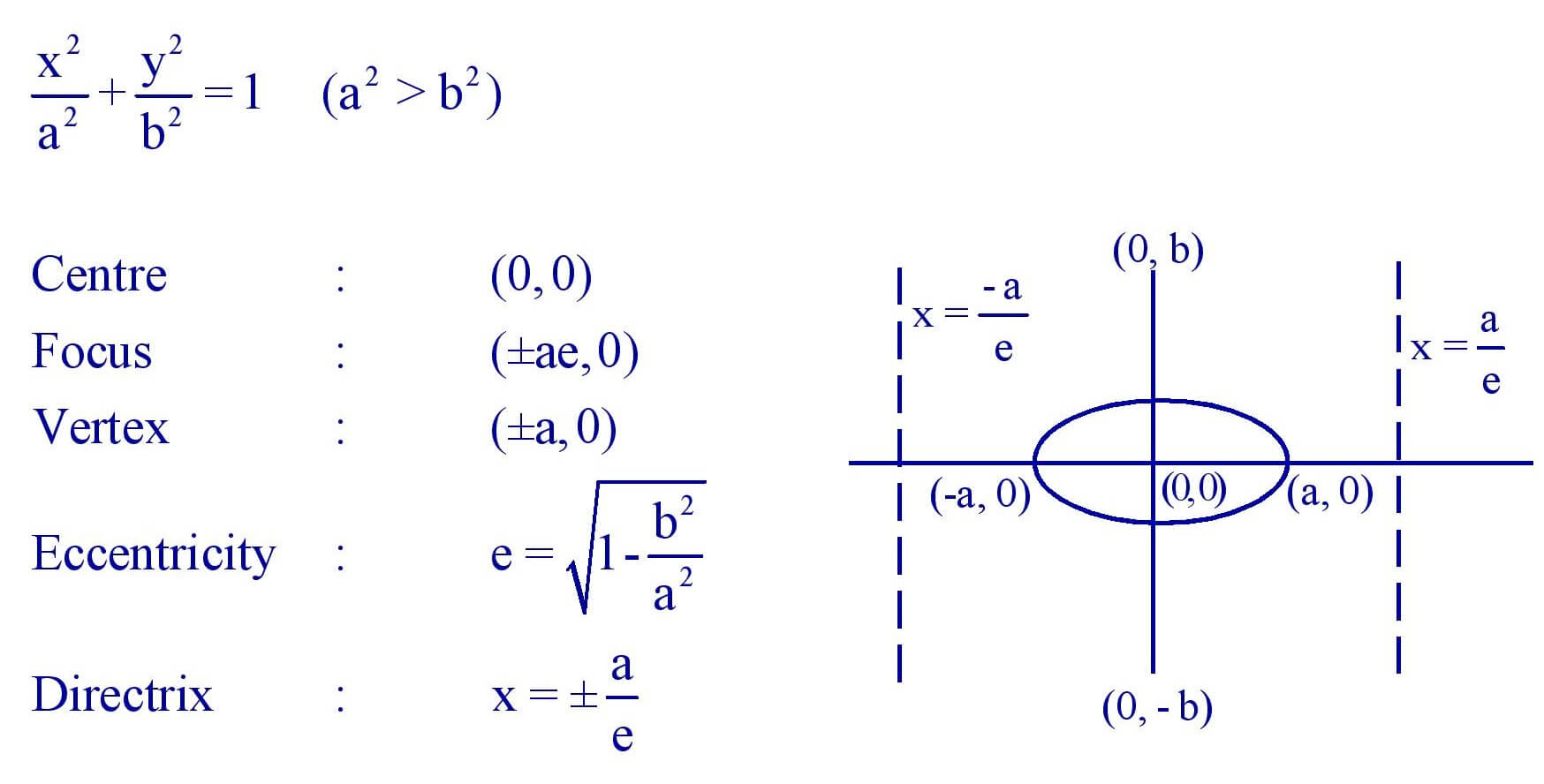
5.11 Monotonic Function :
(i). Increasing Function : Strictly increasing and Non decreasing function.
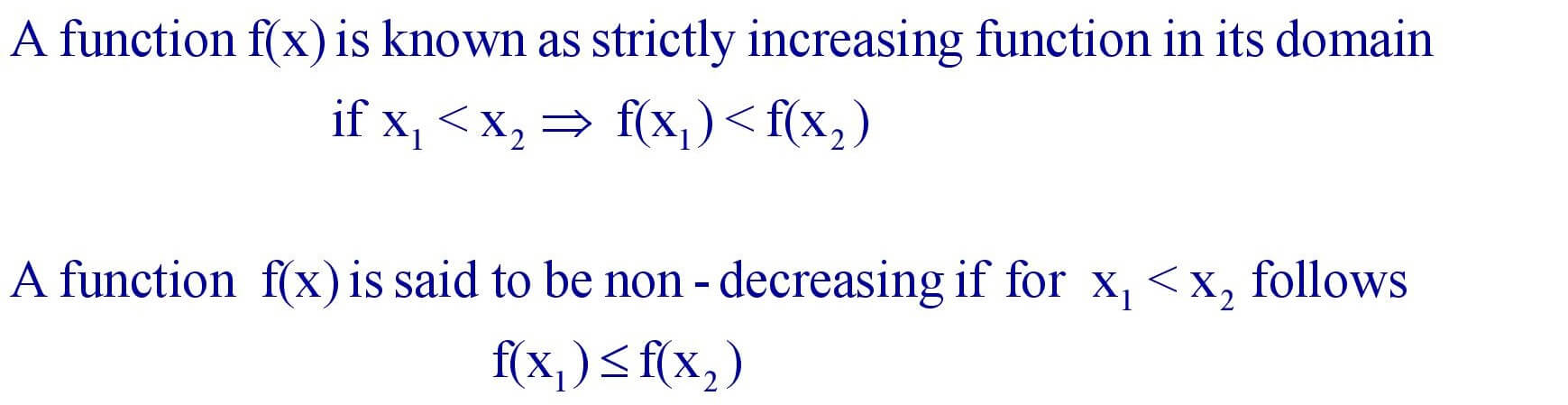
(b). Decreasing Function : Strictly decreasing and Non increasing Function.
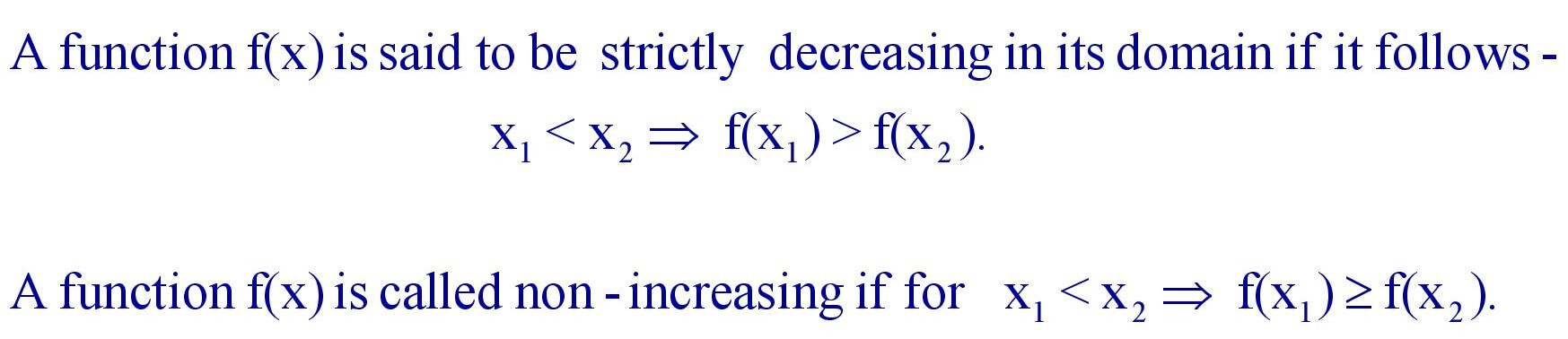
5.12 Periodic Function :
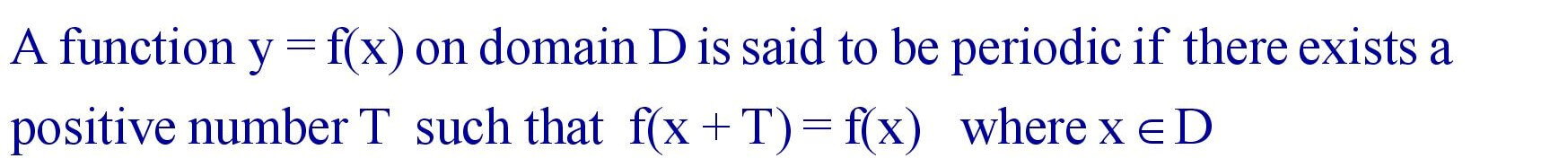
5.13 Composite Function :

Properties of Composite Function :

| Click here to pdf download |
