1. Circle : A Circle is the locus of a point which moves in a plane in such a way that its distance from a given fixed point is always constant.

2. Terms Related to a Circle :
Radius : A line segment joining the centre and a point on the circle is called its radius.

Circumference : The perimeter of a circle is called its circumference.

Chord : A chord of a circle is a line segment joining any two points on the circle.

Diameter : A diameter is a chord of a circle passing through the centre of the circle.

Secant : A line which intersects a circle in two distinct points is called a secant of the circle.

Tangent : A line that intersects the circle in exactly one point is called a tangent to the circle.

3. Position of a point with respect to a Circle.
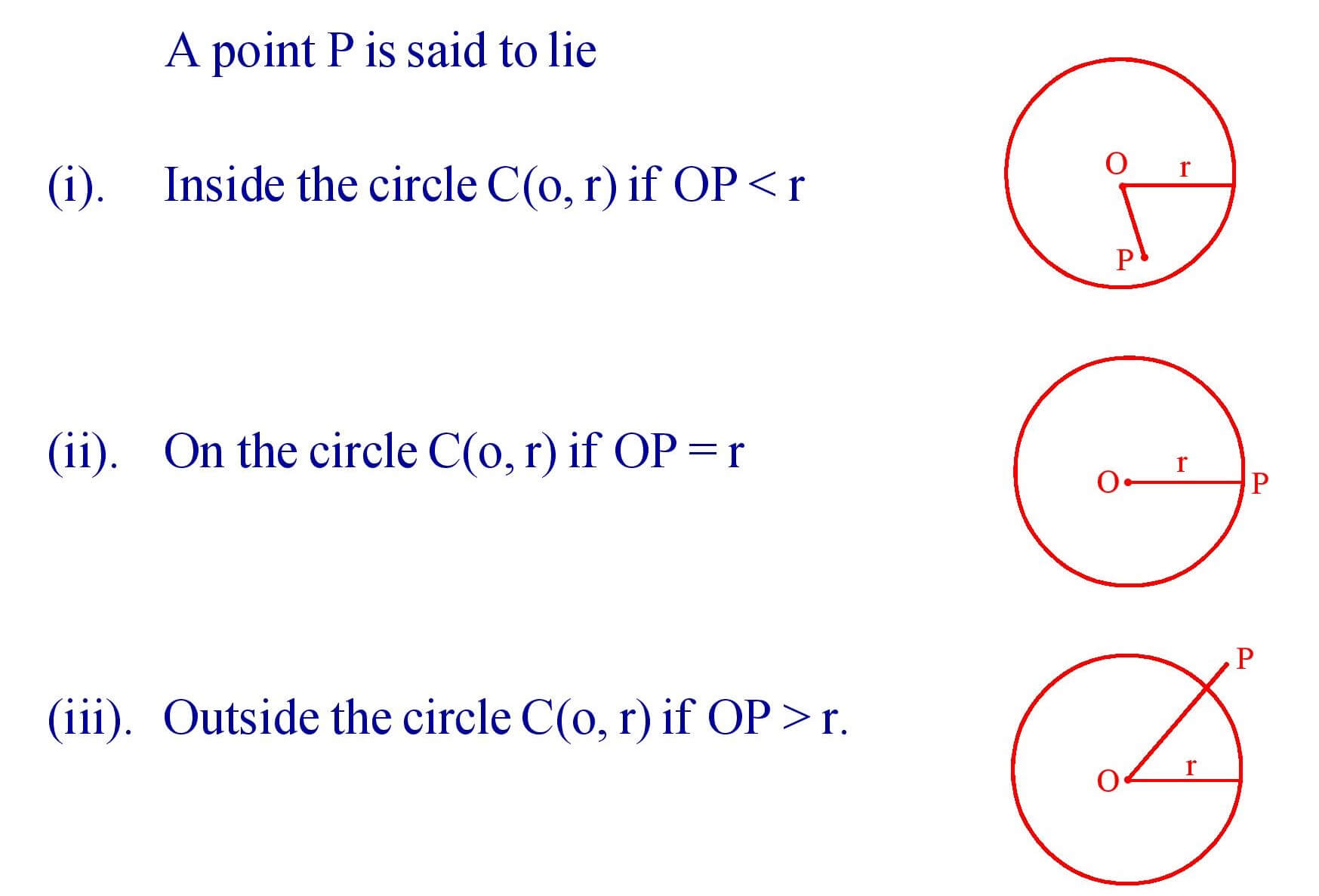
4. Interior of a Circle : The region consisting of all points lying on the circumference of a circle and inside it is called the interior of the circle.
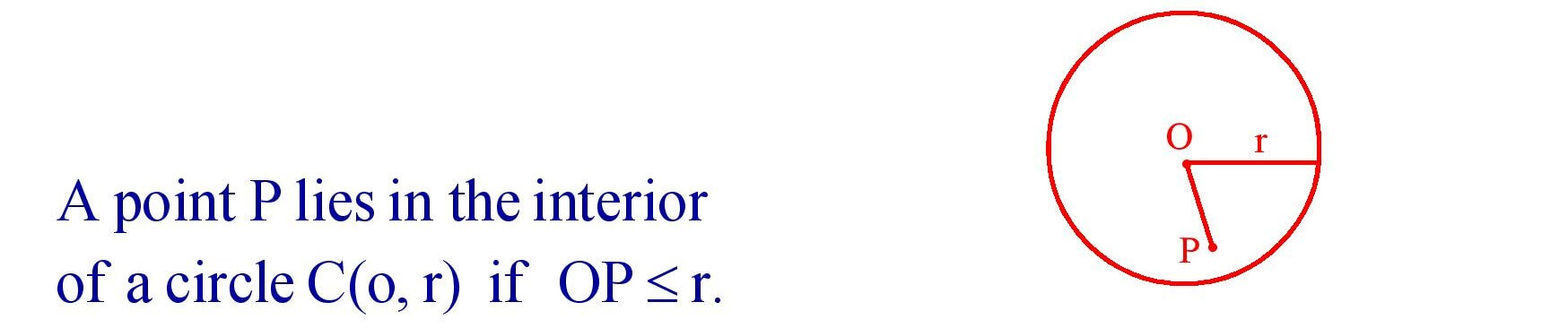
5. Exterior of a Circle : The region consisting of all points lying outside a circle is called the exterior of the circle.

6. Circular Region : The region consisting of all points which are either on the circle or lie inside the circle is called the circular region or circular disc.
7. Concentric Circle : Circles which have the same centre and different radii are called concentric circles.

8. Arc of a Circle : A continuous piece of a circle is called an arc of the circle.

9. Degree Measure of an Arc : Let arc AB be an arc of a circle with centre O.

10. Congruent Arcs : Two arcs AB and CD of a circle are said to be congruent if they have the same degree measures.
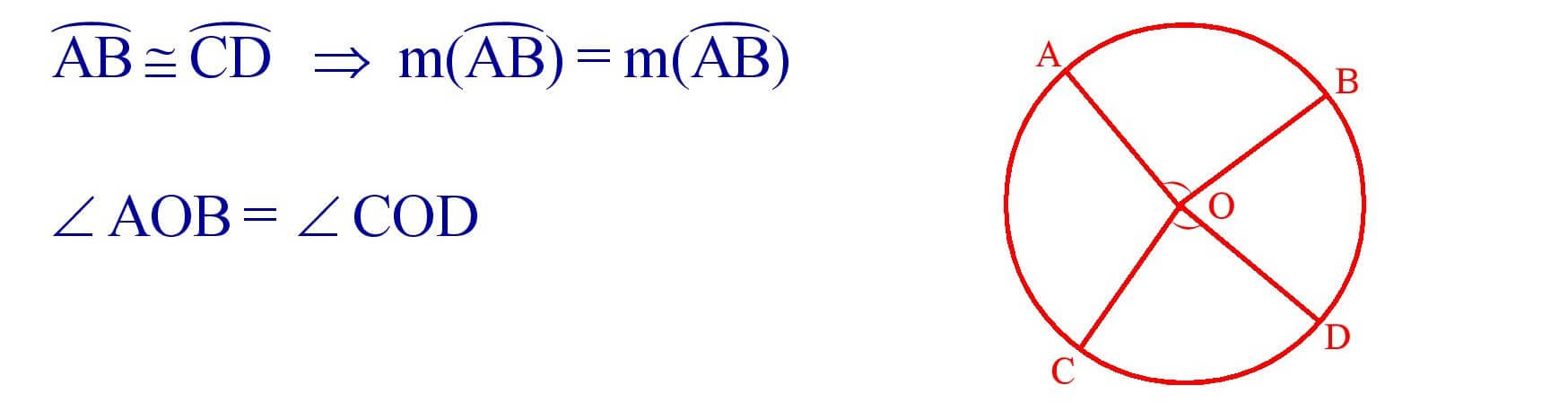
11. Semicircle : A diameter of a circle divides it into two equal arcs.
Each of these two arcs is called a semicircle.
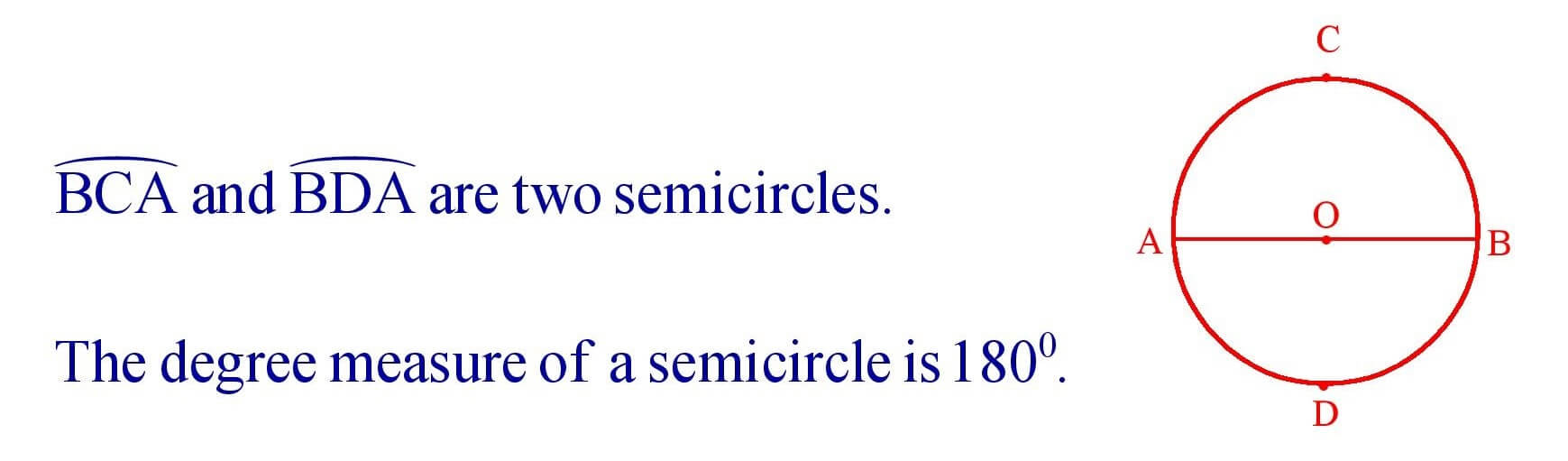
12. Minor arcs of a Circle : If the length of an arc is less than the length of the semicircle then it is called a minor arc.

13. Major arcs of a Circle : If the length of an arc is less than the length of the arc of the semicircle then it is called a minor arc.

14. Segment of a Circle : The part of the circular region bounded by an arc and a chord , including the arc and the chord is called a segment of the circle.
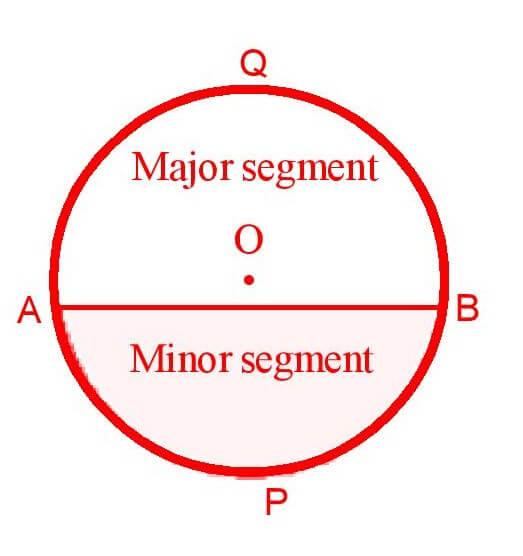
The segment containing the minor arc is called the minor segment and segment containing the major arc is called the major segment.
Thus APBA is the minor segment and AQBA is the major segment of the circle C(o,r).
15. Alternate Segments of a Circle : The minor and major segments of a circle are called the alternate segments of the circle.
16. Sector of a Circle : The region enclosed by an arc of a circle and its two bounding radii is called a sector of the circle.

OABO is the sector of the circle C(o,r)
17. Quadrant of a Circle : One – fourth of a circle is called a quadrant.
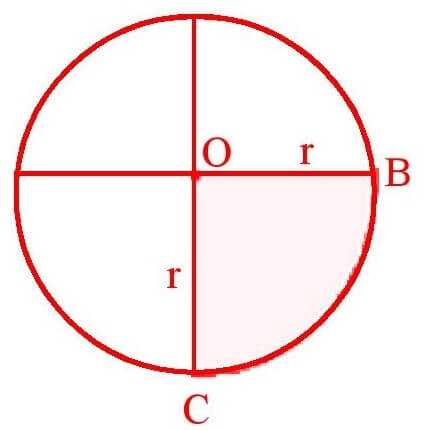
OBCO is a quadrant of the circle C(o,r)
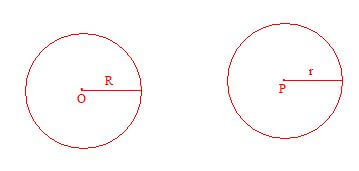
18. Congruent Circles : Two circles C(O, R) and C(P, r) are said to be congruent only when R = r
 19. Cyclic Quadrilateral : A quadrilateral ABCD is said to be cyclic if all its vertices lie on a circle.
19. Cyclic Quadrilateral : A quadrilateral ABCD is said to be cyclic if all its vertices lie on a circle.
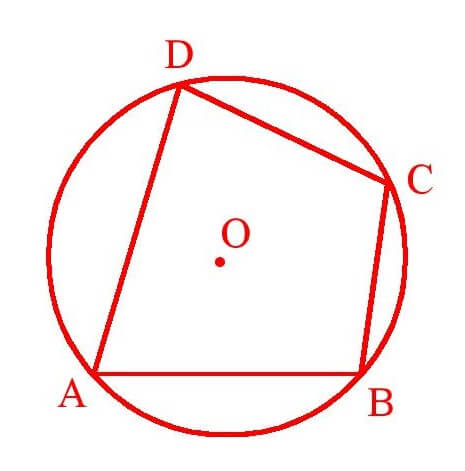
Points lying on a circle are said to be concyclic.
ABCD is a cyclic quadrilateral and hence the points A, B, C , D are concyclic.
Properties of Circle :
1. Two circle are congruent if and only if they have equal radii.

2. Equal chords of a circle subtend equal angles at the centre.

3. If the angles subtended by two chords at the centre of a circle are equal then the chords are equal.

4. If two arcs of a circle are congruent then the corresponding chords are equal.

5. If two chords of a circle are equal then their corresponding arcs are congruent.

6. The perpendicular from the centre of a circle to a chord bisects the chord.
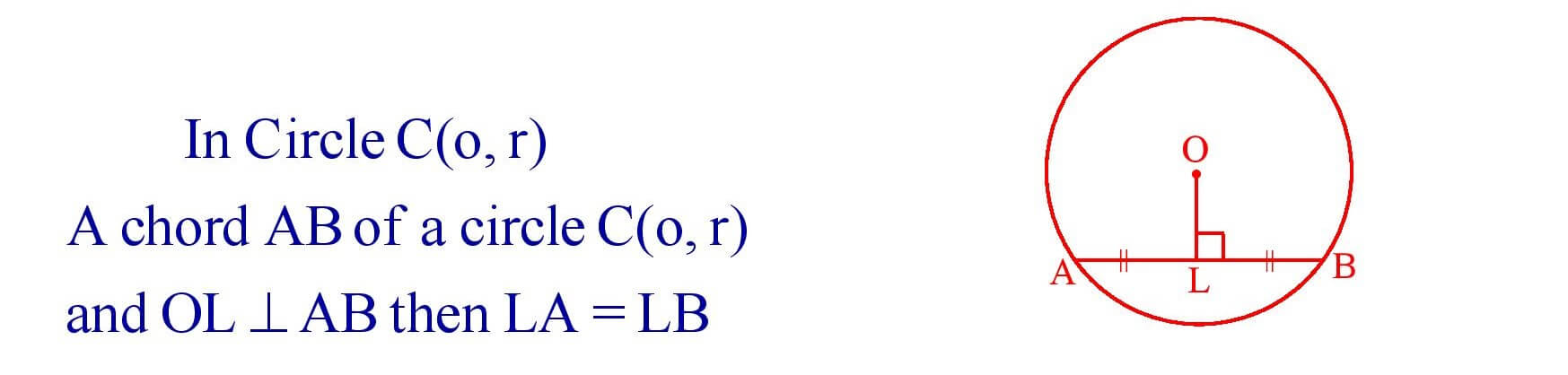
7. The line drawn though the centre of a circle to bisect a chord is perpendicular to the chord.

8. Equal chord of a circle are equidistant from the centre.
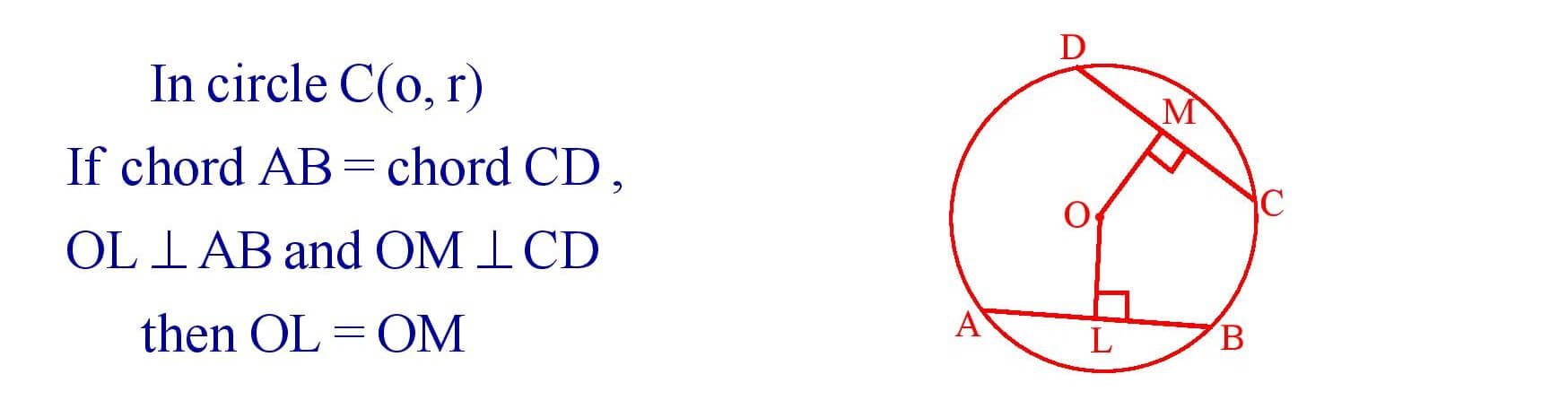
9. The chords of a circle which are equidistant from the centre are equal.

10. There is one and only one circle passing through three given noncollinear points.

11. of any two chords of a circle , the one which is larger is nearer to the centre.

12. of any two chords of a circle , the one which is nearer to the centre is longer.

13. If two arcs of congruent circle are congruent then the corresponding chords are equal.
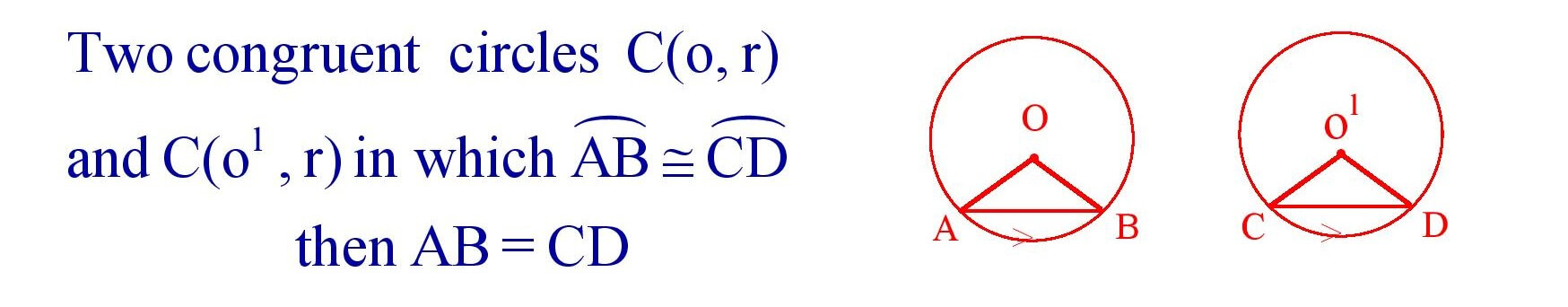
14. If two chords of congruent circles are equal then the corresponding arcs are congruent.
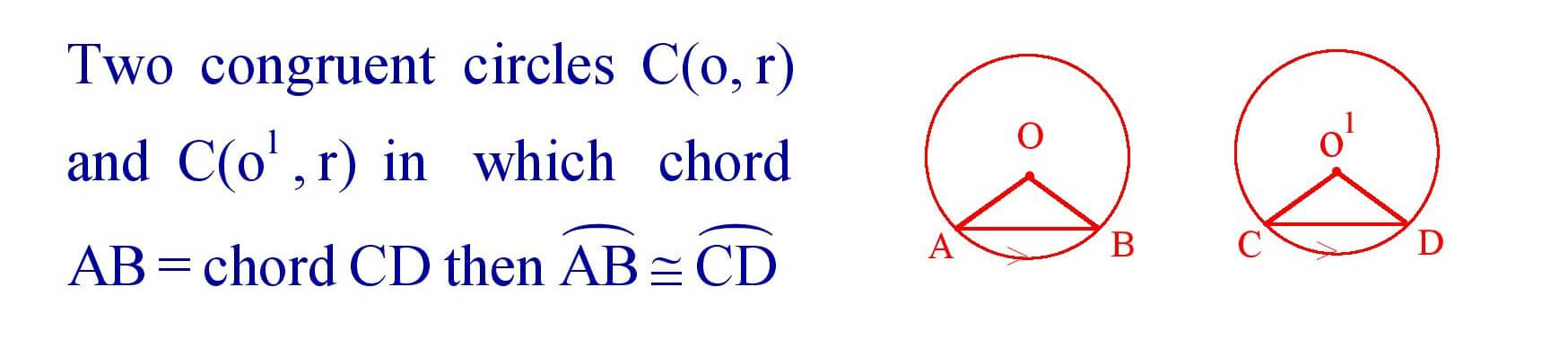
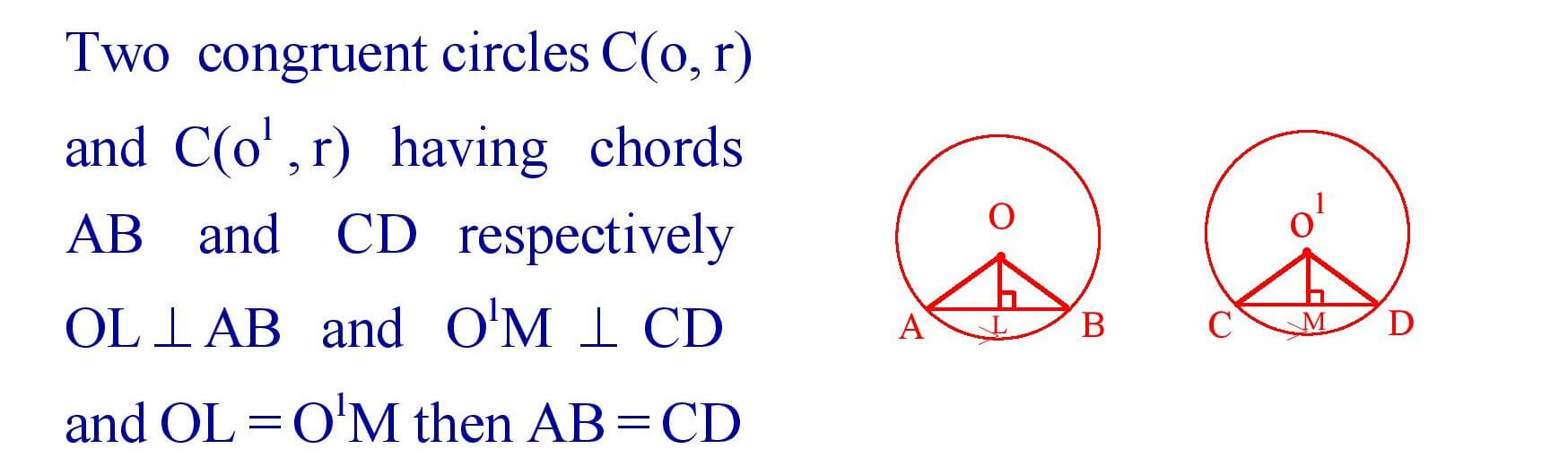
15. Equal chords of congruent circles are equidistant from the corresponding centres.

16. Chords of congruent circles which are equidistant from the corresponding centres are equal.
17. Equal chords of congruent circles subtend equal angles at the centre.
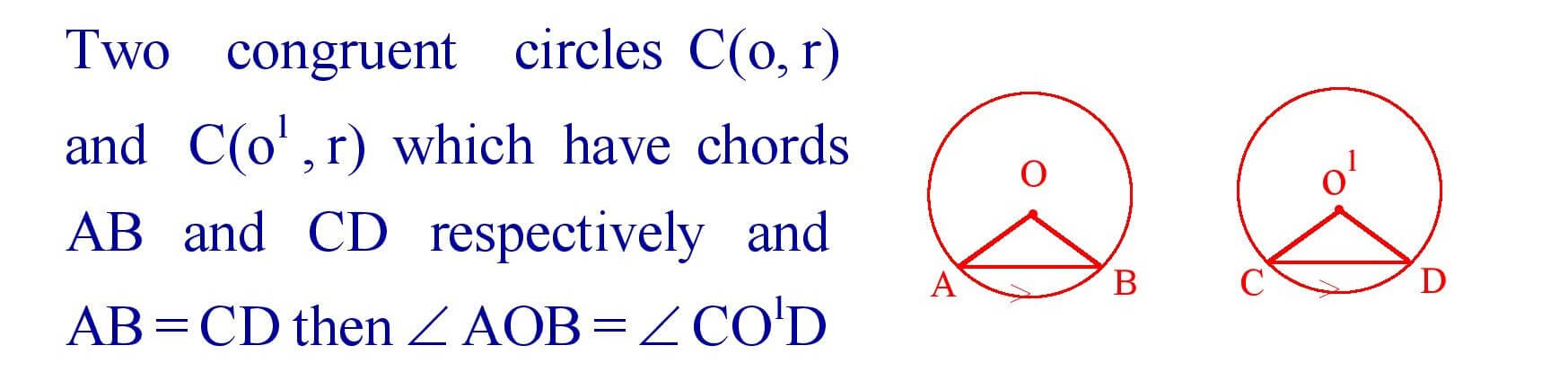
18. If the angles subtended by the chords of congruent circles at the corresponding centres are equal then the chords are equal.

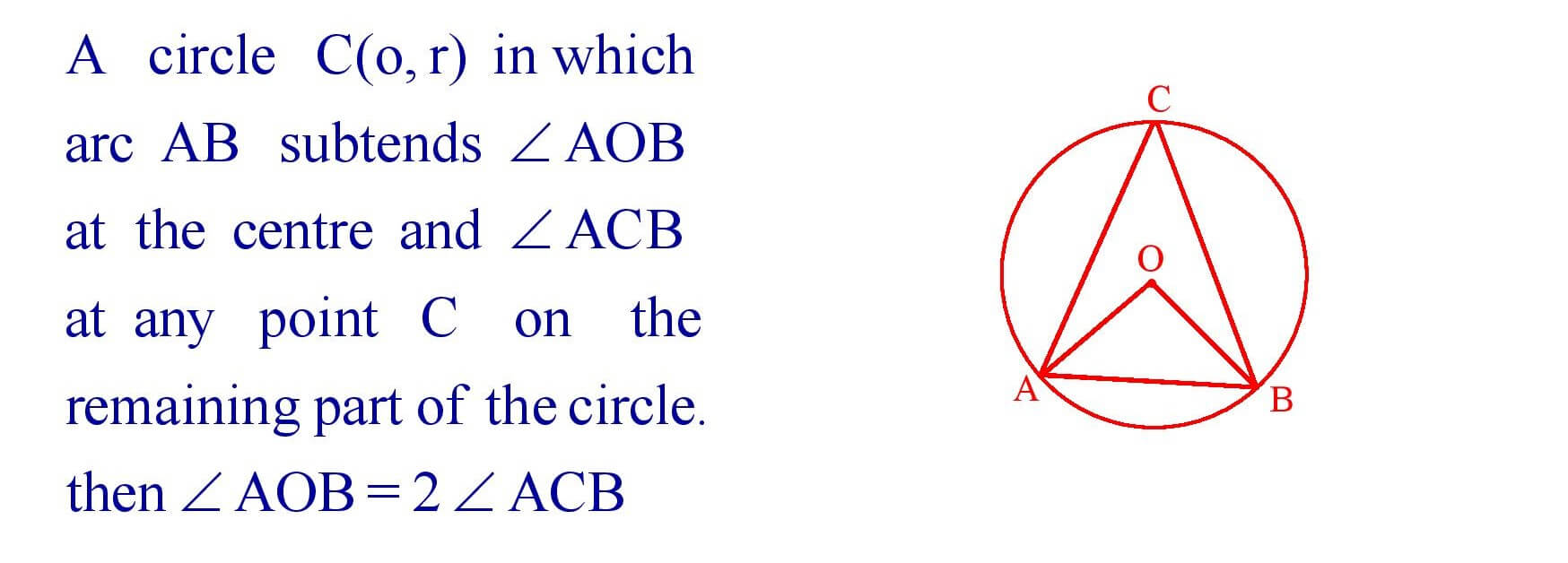
19. The angle subtended by an arc of a circle at centre is double the angle subtended by its any point on the remaining part of the circle.
20. The angle in a semicircle is a right angle.

21. The arc of a circle subtending a right angle at any point of the circle in its alternate segment is a semicircle.

22. Angles in the same segment of a circle are equal.
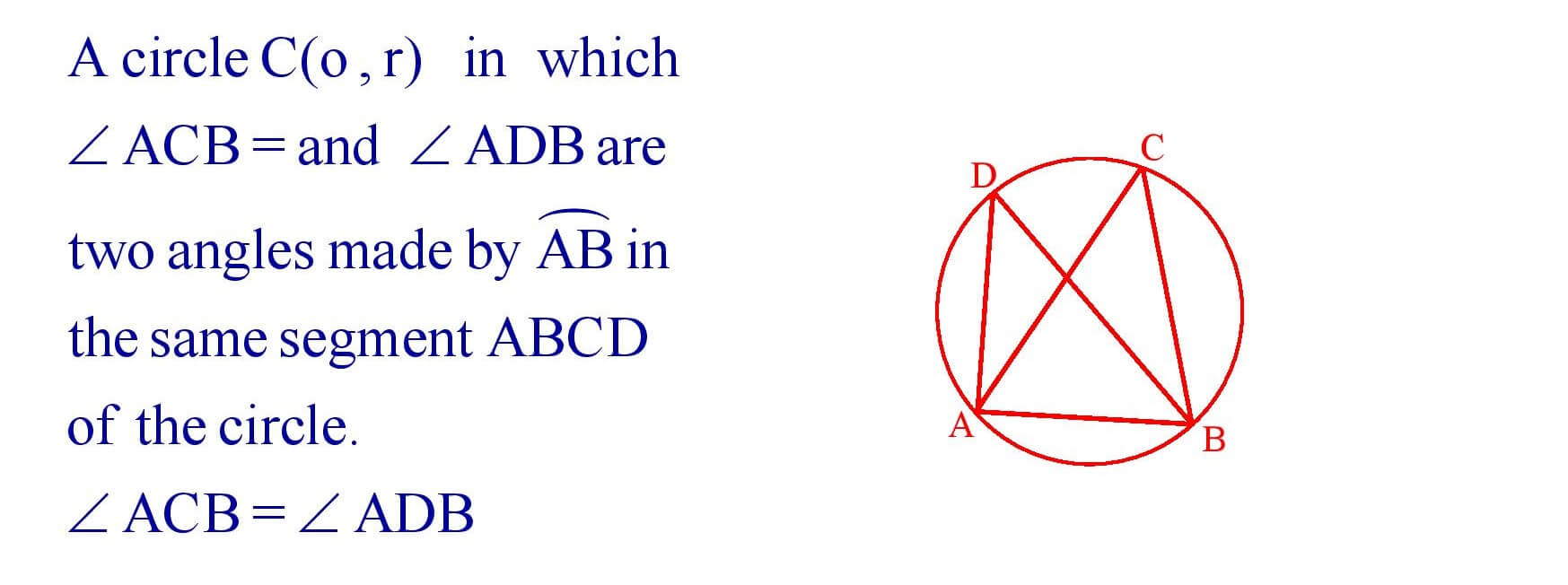
23. If a line segment joining two points subtends equal angles at two other points lying on the same side of the line segment then the four points are concyclic or lie on the same circle.

24. The sum of either pair of the opposite angles of a cyclic quadrilateral is 1800.

25. If a pair of opposite angles of a quadrilateral is supplementary then the quadrilateral is cyclic.

26. If one side of a cyclic quadrilateral is produced then the exterior angle is equal to the interior opposite angle.

| Click here to pdf download |
