Sets Formula For 11th Class

1. Sets :

2. Some Standard Notations for Some Special Sets :

3. Representation of Sets : There are two methods to represent a set

(i). Roster or Tabular form or Enumeration Method :

(ii). Set builder form or Rule Property method :

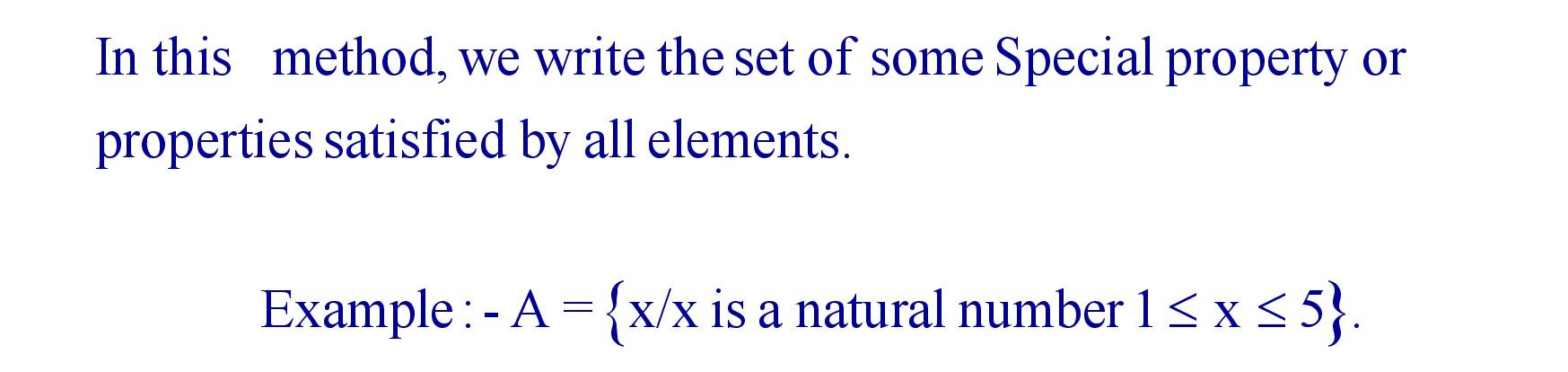
4. Types of Sets :

(i). Empty Set or Null Set or Void Set :

Note :

(ii). Singleton Set :

(iii). Pair Set or Doubleton Set :

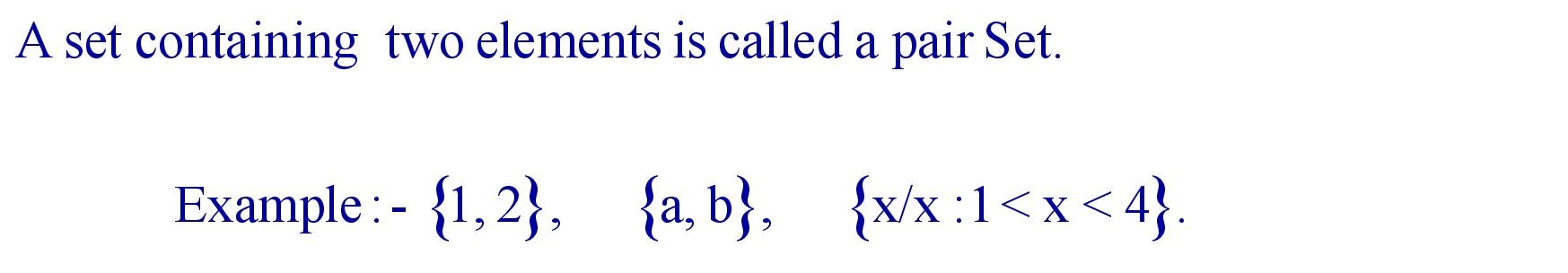
(iv). Finite Set :

(v). Cardinal Number of a Finite Set :

(vi). Infinite Set :

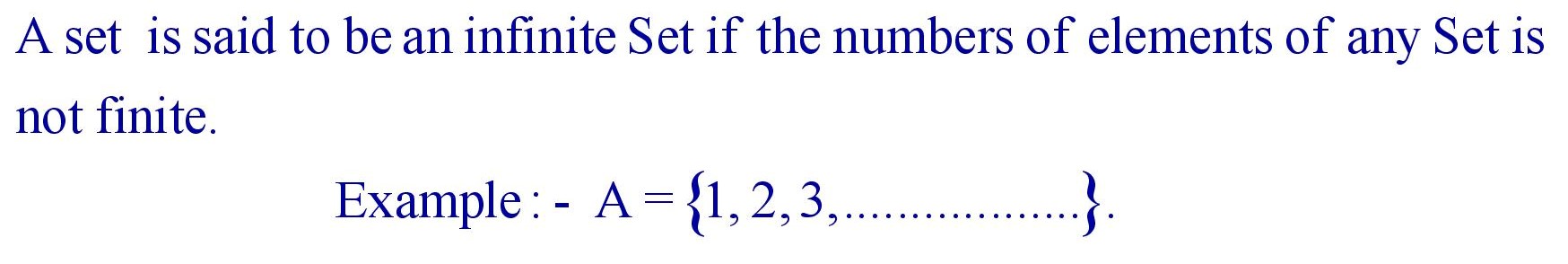
(vii). Equivalent Sets :

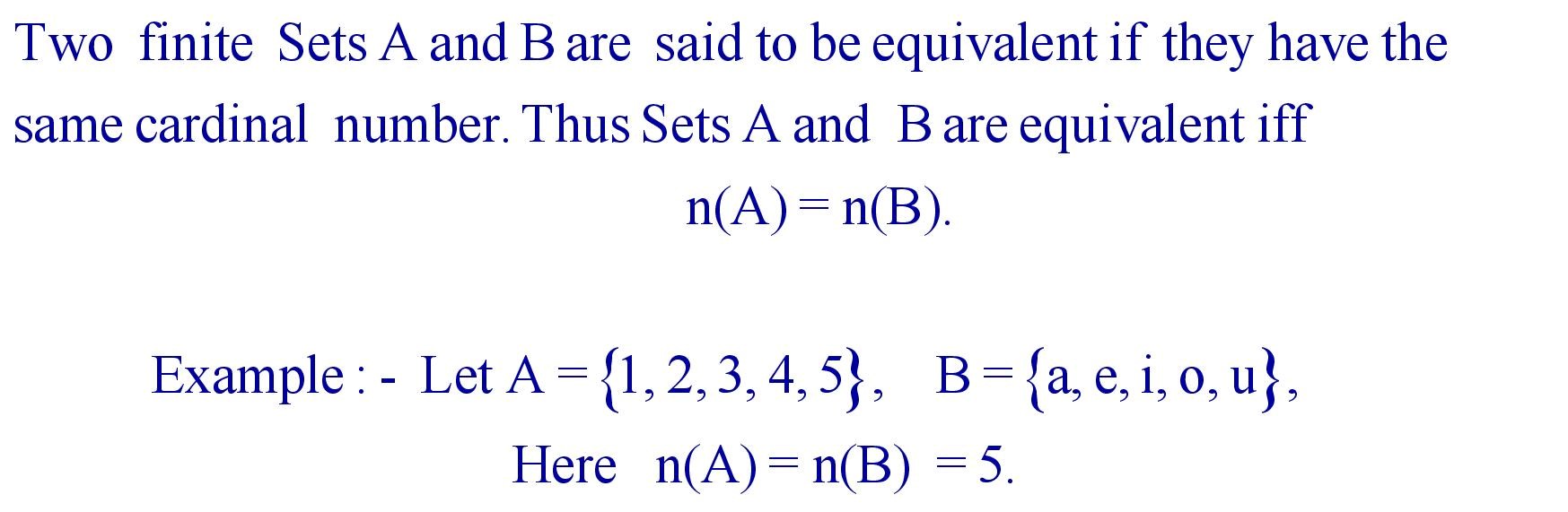
(viii). Equal Sets :

(ix). Set of Sets :

(x). Super Set :

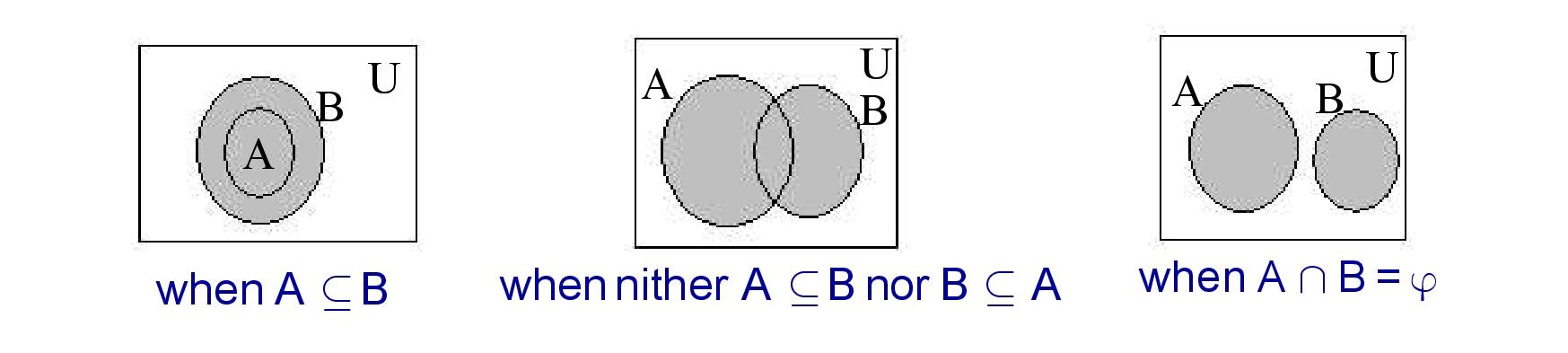
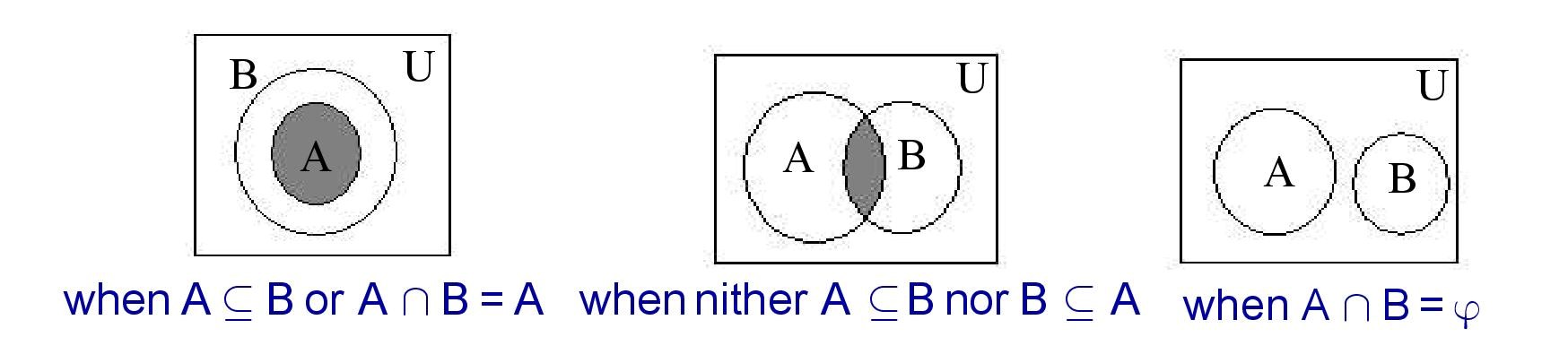
(xi). Subsets :

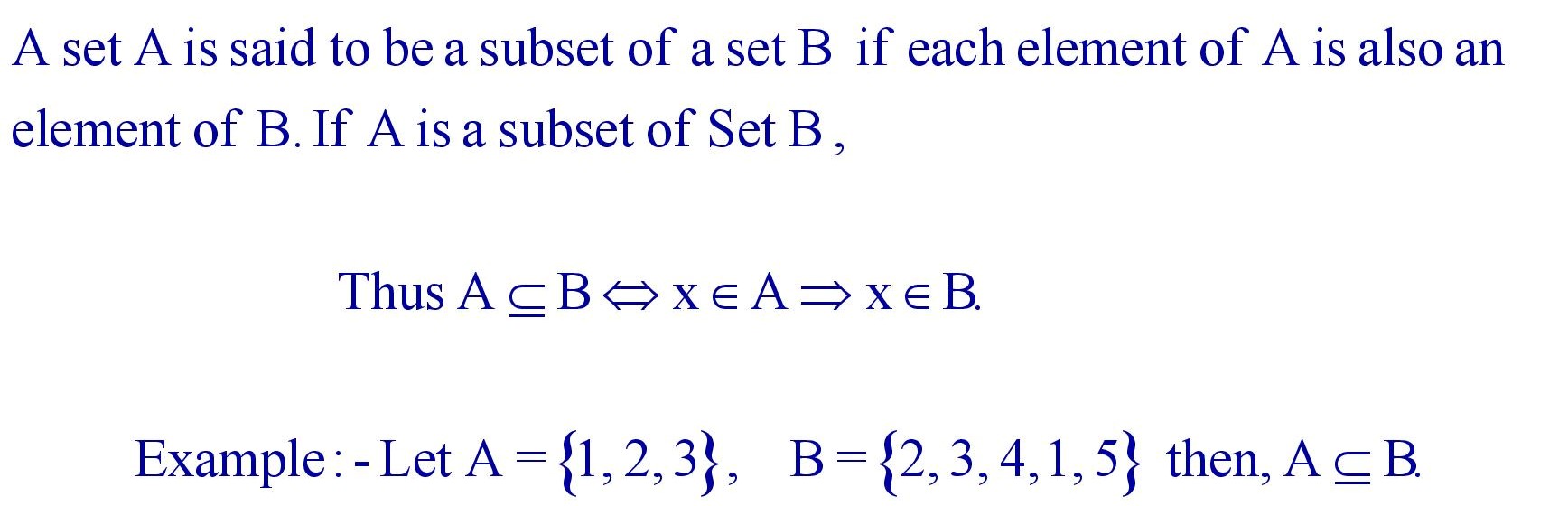
(xii). Proper Subset :

Note :

(xiii). Power Set :

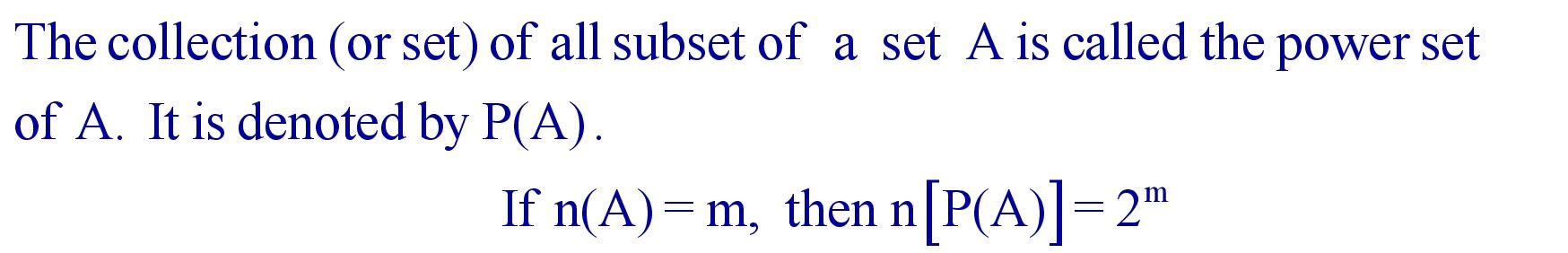
(xiv). Universal Set :

5. Venn Diagrams :

6. Operation of Sets :

(i). Union of two Sets :

Venn Diagram of A∪B : 

(ii). Intersection of two Sets : 

Venn Diagram of A ∩ B :

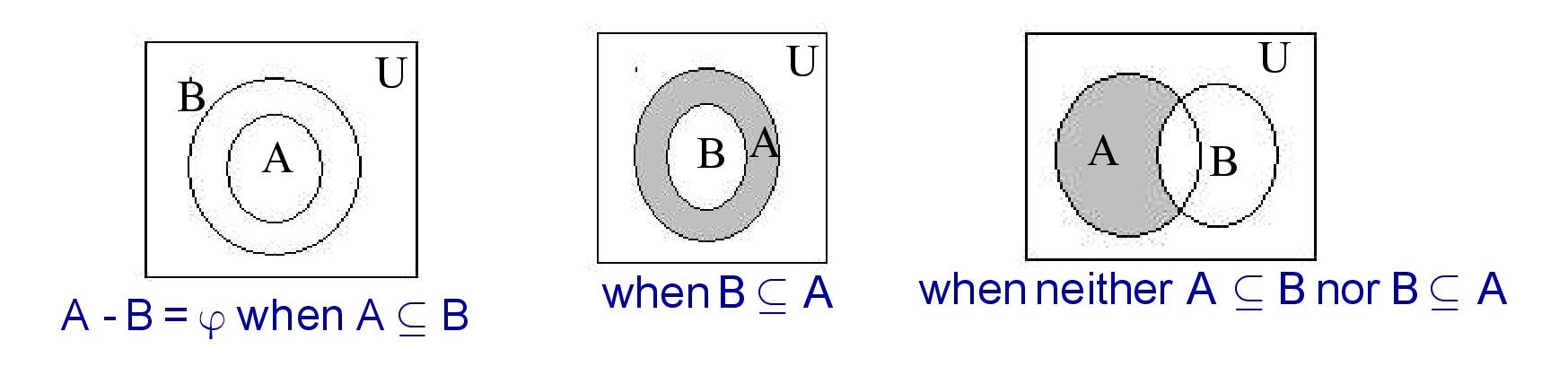
(iii). Difference of Sets : 

Venn Diagram of A – B :

(iv). Symmetric Difference of two Sets :

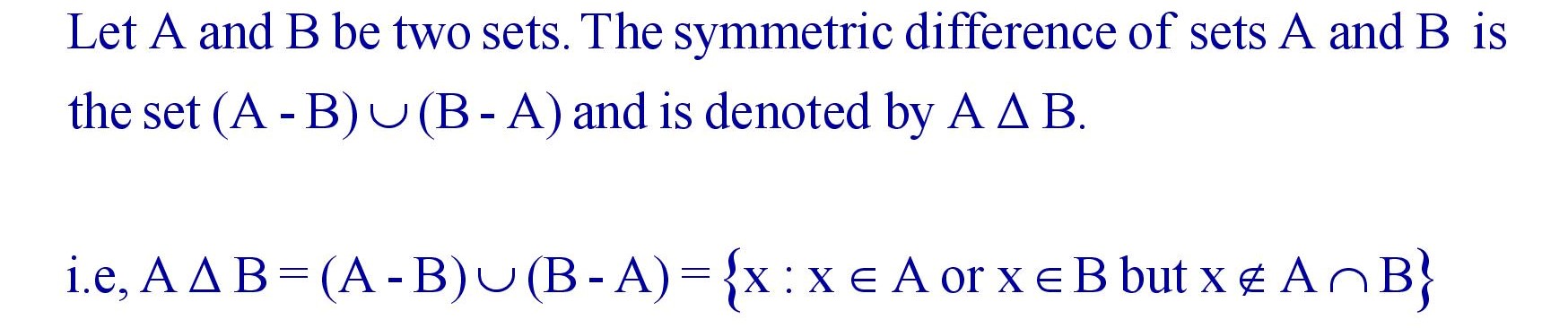
Venn Diagram of A Δ B :

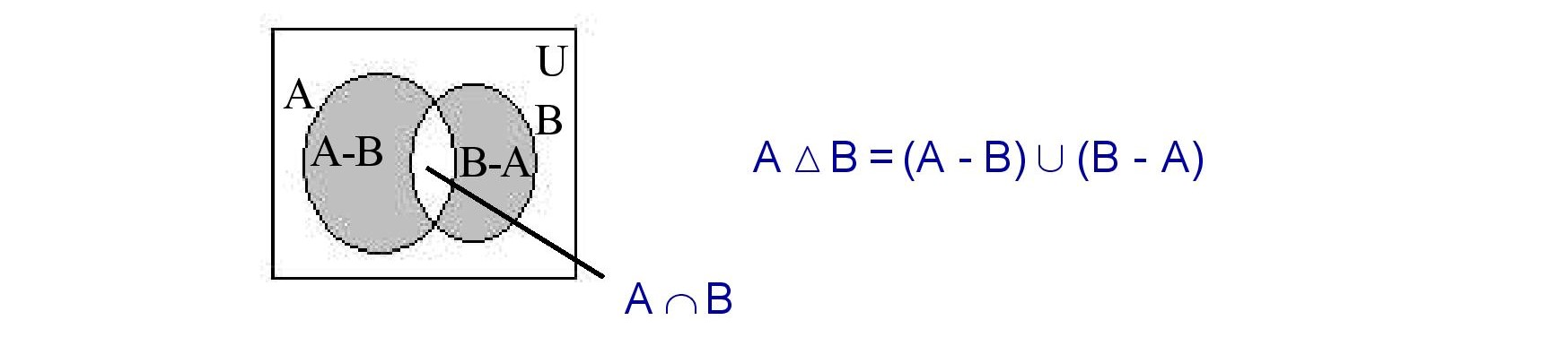
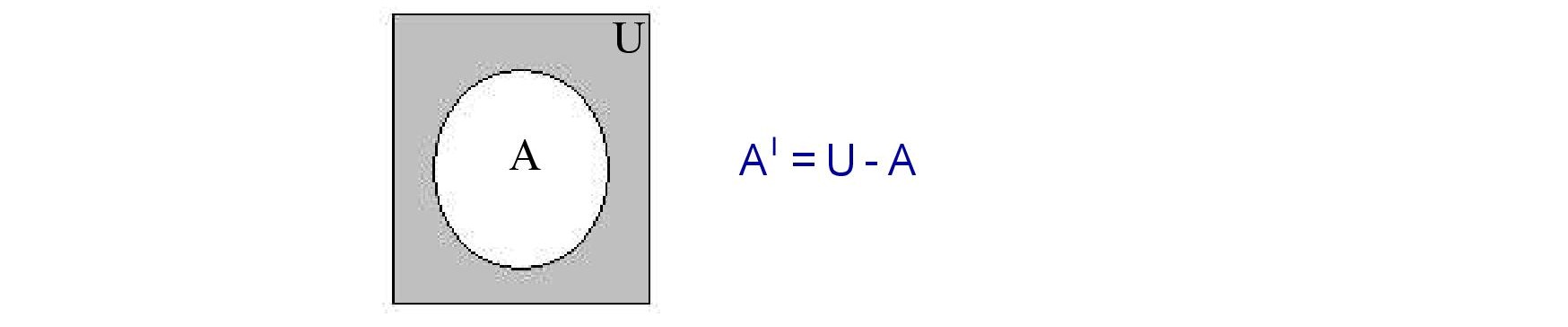
(v). Complement of a Set :

Venn Diagram of A^l

7. Some Important Laws of Sets :

(i). Idempotent Laws : For any set A.

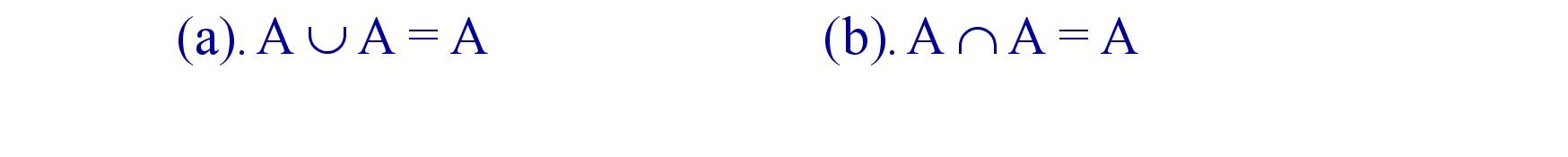
(ii). Identity Laws : For any set A.

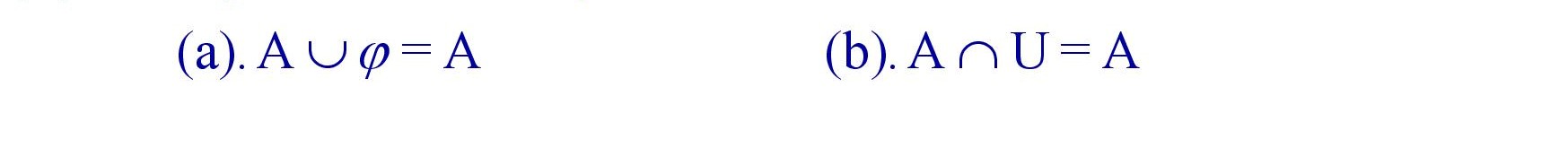
(iii). Commutative Laws : For any two sets A and B.

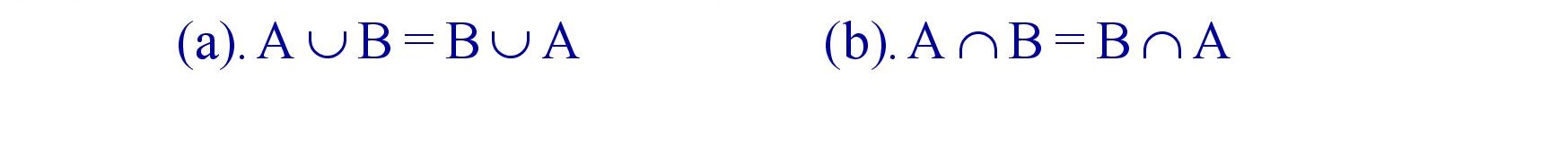
(iv). Associative Laws : For any three sets A and B.

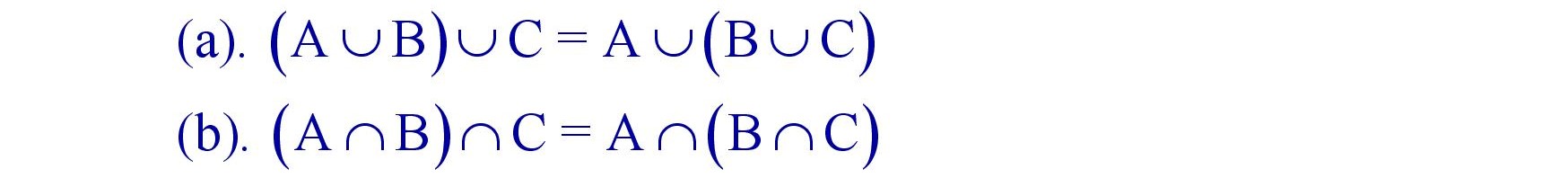
(v). Distributive Laws :

(vi). De – Morgan’s Law : For any two sets A and B.

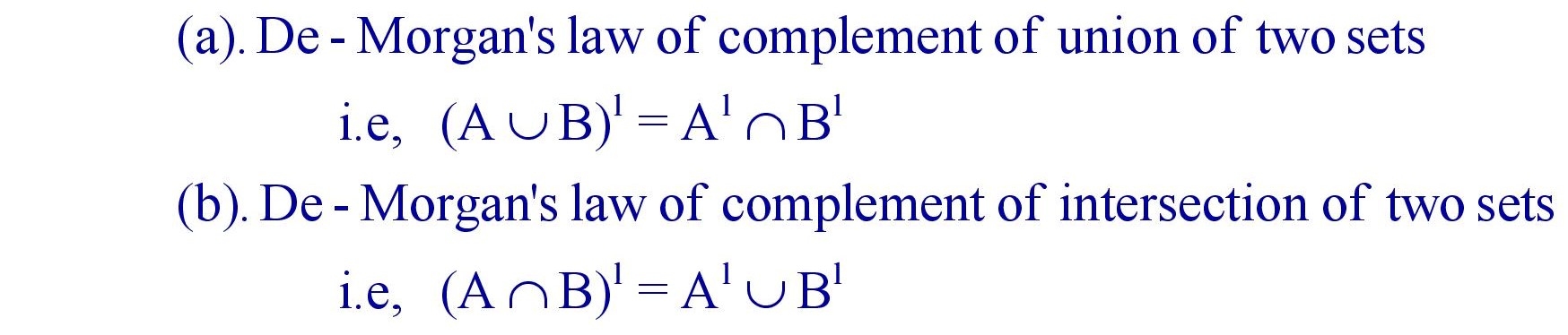
8. Some Important Theorems :

9. Formula for Sets :

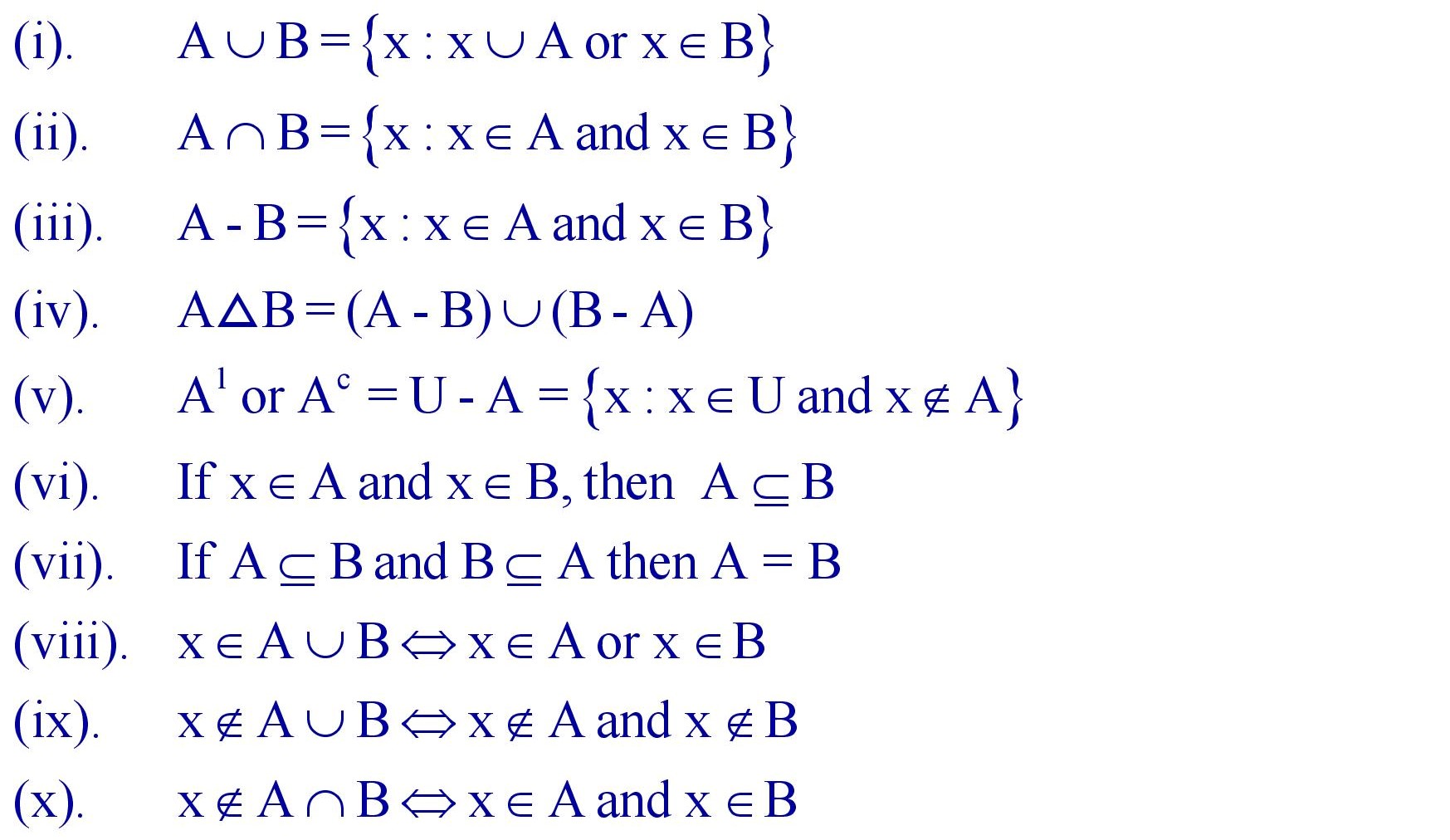
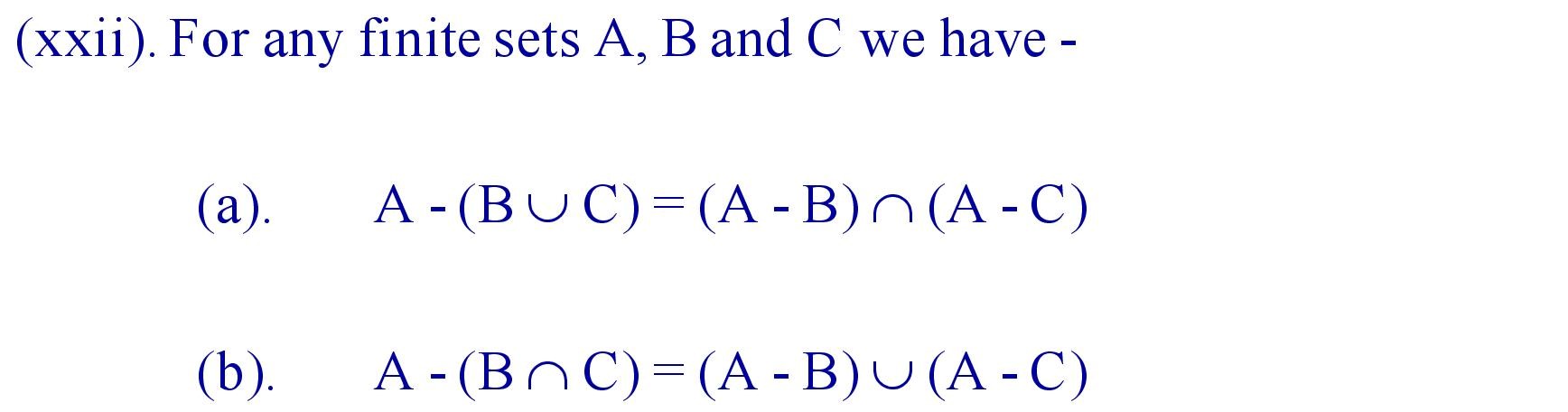
Click here to pdf download