सिद्धांत संख्या – 1
यदि किसी वृत्त अथवा सर्वांगसम वृतों के दो चाप सर्वांगसम हो , तो संगत जीवाएँ समान होती है।

सिद्धांत संख्या – 2
यदि किसी वृत्त अथवा सर्वांगसम वृतों के दो चाप समान हो , तो संगत जीवाएँ समान होती है।

सिद्धांत संख्या – 3
वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है।

सिद्धांत संख्या – 4
वृत्त के केंद्र और जीवा के मध्य बिंदु को मिलाने वाली रेखा जीवा पर लंब होती है।

सिद्धांत संख्या – 5
तीन असंरेख बिंदुओं से होकर एक और केवल एक वृत्त जाता है।

सिद्धांत संख्या – 6
वृत्त की समान जीवाएँ केंद्र से समदूरस्थ होती है।
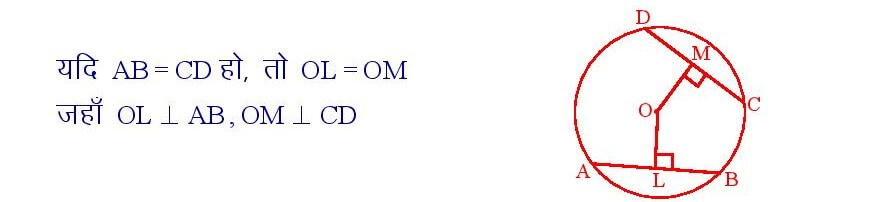
सिद्धांत संख्या – 7
किसी वृत्त की दो जीवाओं में से बड़ी , छोटी की अपेक्षा केंद्र से निकटतर होती है।

सिद्धांत संख्या – 8
वृत्त के एक चाप का अंशमाप चाप के सापेक्ष वृत्त के एकांतर खंड के किसी एक बिंदु पर इस चाप द्वारा अंतरित कोण का दुगना होता है।

सिद्धांत संख्या -9
वृत्त के एक ही खंड के कोई दो कोण बराबर होते हैं।

सिद्धांत संख्या – 10
अर्धवृत्त का कोण समकोण होता है।
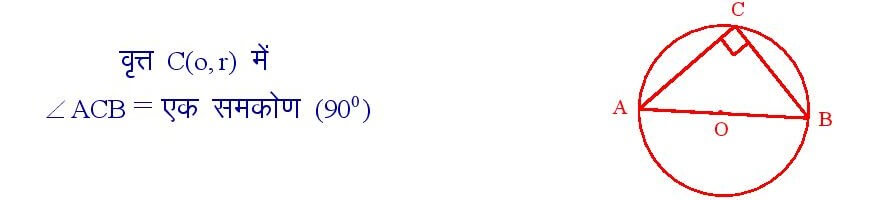
सिद्धांत संख्या – 11
एकांतर खंड में किसी वृत्त के लघु चाप द्वारा आंतरिक कोण न्यून कोण होता है और एकांतर खंड में दीर्घ चाप द्वारा अंतरित कोण अधिककोण होता है।

सिद्धांत संख्या – 12
अपने एकांतर खंड में वृत्त के किसी बिंदु पर समकोण अंतरित करने वाला वृत्त का चाप अर्धवृत्त होता है।

सिद्धांत संख्या – 13
यदि दो बिंदुओं को मिलानेवाली रेखाखंड दो अन्य बिंदुओं पर जो इस रेखाखंड को आविष्ट करने वाली रेखा के एक ओर स्थित है , समान कोण अंतरित करता हो तो ये चार बिंदु एकवृत्तीय हैं ।
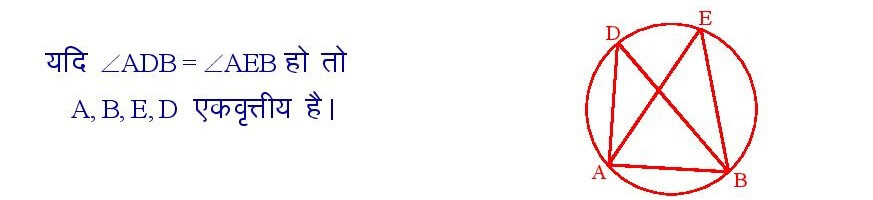
सिद्धांत संख्या – 14
वृतों अथवा सर्वांगसम वृतों की बराबर जीवाएँ केंद्र अथवा संगत केद्रों पर बराबर कोण अंतरिक करती है।

सिद्धांत संख्या – 15
यदि वृत्तों अथवा सर्वांगसम वृत्तों की दो जीवाओं द्वारा केंद्र अथवा संगत केंद्रों पर अंतरित कोण बराबर हो तो वे जीवाएँ आपस में बराबर होती है।
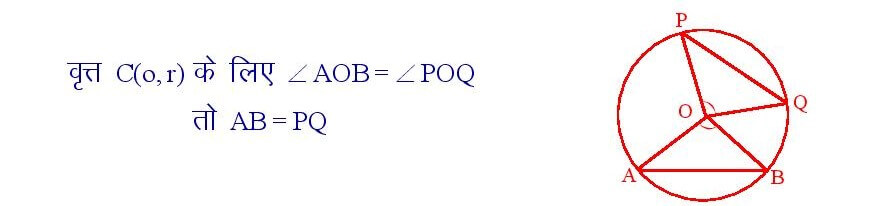
सिद्धांत संख्या – 16
चक्रीय चतुर्भुज के सम्मुख कोणों के किसी भी युग्म का योगफल 1800 होता है।
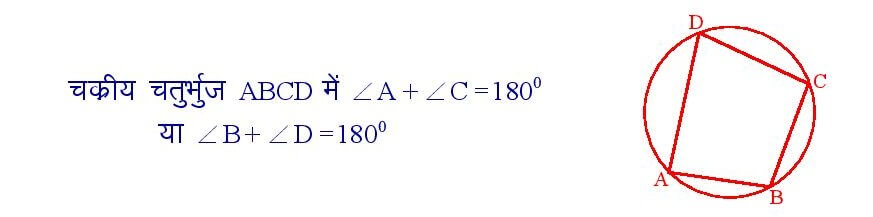
सिद्धांत संख्या – 17
यदि किसी चतुर्भुज के सम्मुख कोणों का युग्म संमपूरक हो , तो चतुर्भुज चक्रीय होता है।

सिद्धांत संख्या – 18
वृत्त की स्पर्शरेखा के स्पर्शबिंदु पर वृत्त की त्रिज्या लंब होती है।

सिद्धांत संख्या – 19
वह रेखा जो त्रिज्या के छोरबिंदु से होकर जाती है और इसपर लंब है, वृत्त की स्पर्श रेखा होती है।

सिद्धांत संख्या – 20
किसी बाह्य बिंदु से वृत पर खींची गई दो स्पर्श रेखाओं की लंबाईयाँ बराबर होती है।

सिद्धांत संख्या – 21
यदि किसी वृत्त की दो जीवाएँ वृत्त के अंदर या बढ़ाने पर बाहर प्रतिच्छेद करती हो तो एक जीवा के दो खंडों से बने आयत का क्षेत्रफल दूसरी जीवा के दो खंडों से बने आयत के क्षेत्रफल के बराबर होता है।

सिद्धांत संख्या – 22
यदि PAB वृत्त की छेदक रेखा है जो वृत्त को A और B पर प्रतिच्चेद करती हो और PT एक स्पर्श रेखाखंड हो तो
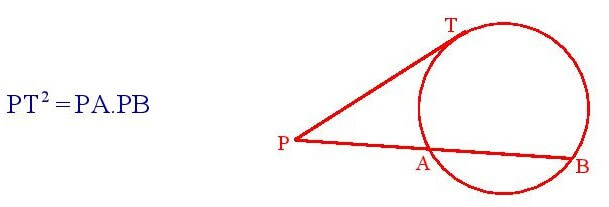
सिद्धांत संख्या – 23
यदि वृत्त की स्पर्श रेखा के स्पर्शबिंदु से एक जीवा खींची जाए तो इस जीवा द्वारा दी हुई स्पर्श रेखा के साथ बनाए गए कोण, संगत एकांतर खंडों में बनाए गए कोण के क्रमश: बराबर होते हैं।

सिद्धांत संख्या – 24
यदि वृत्त की जीवा एक छोरबिंदु से होती हुई खींची गई रेखा और जीवा के बीच का कोण एकांतर खंड में जीवा द्वारा अंतरित कोण के बराबर हो तो यह रेखा वृत्त की स्पर्श रेखा होती है।

सिद्धांत संख्या – 25
यदि दो वृत्त एक दूसरे को आंतरिक या बाह्यतः स्पर्श करते हों तो यह स्पर्शबिंदु केंद्रों से होकर जाने वाली रेखा पर स्थित होता है।

सिद्धांत संख्या – 26
यदि दो वृत्त एक बिंदु पर स्पर्श करते हों तो इन वृत्तों के स्पर्शबिंदु पर एक उभयनिष्ठ स्पर्श रेखा होती है।

नोट : –
- किसी वृत्त की त्रिज्याएँ आपस में बराबर होती है।
- किसी वृत्त की सभी व्यास आपस में बराबर होते हैं।
- एक वृत्त का एक ही केंद्र हो सकता है।
- यदि कोई बिंदु वृत्त के बाहर हो तो केंद्र से उसकी दूरी त्रिज्या की लंबाई से बड़ी होगी।
- यदि कोई बिंदु वृत्त के भीतर हो तो केंद्र से उसकी दूरी त्रिज्या की लंबाई से कम होगी।
- यदि केंद्र और त्रिज्या ज्ञात हो तो वृत्त पूरी तरह निर्माण हो जाता है।
- वृत्त एक बंद वक्र है जिसे एक सरल रेखा साधारणतः दो बिंदुओं पर काटती है।