Compound Angle Formula : Algebraic sum of two or more angles is called compound angle.
If A, B and C are any angle then A + B , A + B + C, A – B + C, A + B – C, A – B – C, A – B ………..etc are all compound angles.
Addition of Compound Angle Formula :
- Sin (A + B) = SinA.CosB + CosA.SinB
- Sin (A + B) = SinA.CosB + CosA.SinB
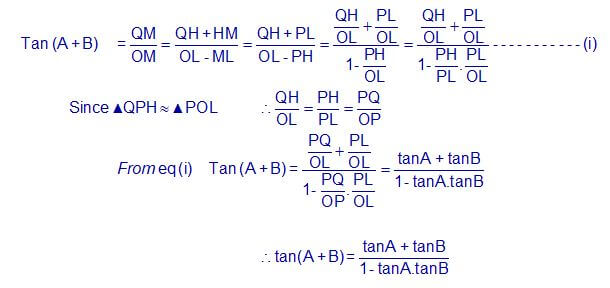
- Tan (A + B) = TanA + TanB/ 1 – TanA.TanB
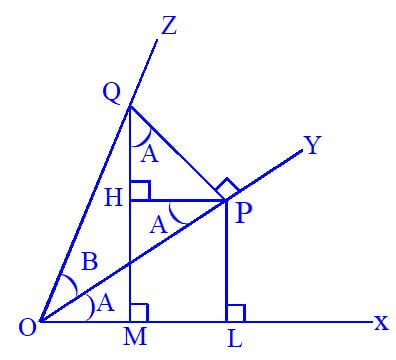
Let the revolving line starting from the position ox with angle A and again revolving in same direction with angle B.
∴ ∠ Xoy = A and ∠Xoy = B then ∠XOZ = A + B Let Q be a any point on oz.
Draw QM ⊥ OX and QP ⊥ OY from point Q. Draw PH ⊥ QM from Point P
Now ∠HPO = ∠POX = A ∴ ∠HPO = 90o
∠ HPO = 90o – A ∴ ∠HQP = A
In Δ QOM


Subtraction of Compound Angle Formula :
- Sin (A – B) = SinA.CosB – CosA.SinB
- Sin (A – B) = SinA.CosB – CosA.SinB
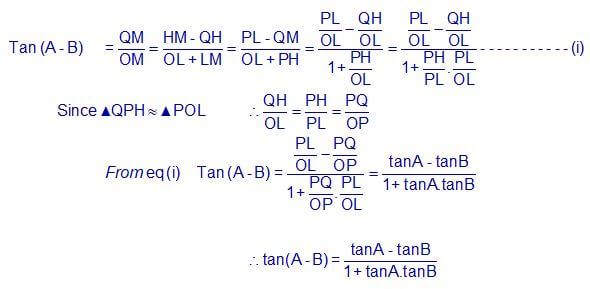
- Tan (A – B) = TanA – TanB/ 1 + TanA.TanB
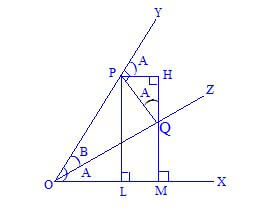
Let the revolving line starting from the position ox with angle A and again revolving in opposite direction with angle B.
∴ ∠ Xoy = A and ∠Xoy = B then ∠XOZ = A – B Let Q be a any point on oz.
Draw QM ⊥ OX and QP ⊥ OY from point Q. Draw PH ⊥ QM from Point P.
Now ∠YPH = ∠POX = A ∴ ∠QPY = 90o
∠ QPH = 90o – A ∴ ∠HQP = A
In Δ QOM
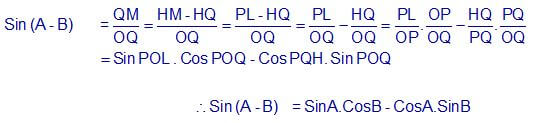

Compound Angle Formula :



