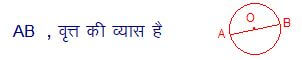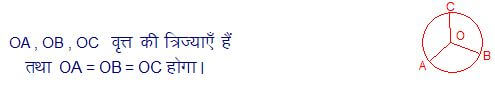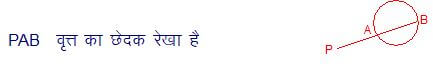ज्यामिति का परिचय
” ज्यामिति” शब्द दो शब्दों के योग से बना है ज्या + मिति । ‘ ज्या का अर्थ है जमीन और मिति का अर्थ है ” माप ” । इसलिए यह स्पष्ट कहा जा सकता है कि ज्यामिति की शुरुआत जमीन नापने के संदर्भ में हुई होगी। ऐसा विश्वास किया जाता है कि प्राचीन समय में मिश्र और बेबिलोनिया के निवासियों ने सबसे पहले करीब 2500 वर्ष पूर्व ज्यामिति का अध्ययन शुरू किया था । वे ज्यामिति का उपयोग अधिकतर व्यावहारिक कार्यों में जैसे भूमि को नापने में करते थे और इसके क्रमबद्ध अध्ययन की दिशा में इन्होंने बहुत कम योगदान दिया । इसके बाद सम्भवतः ज्यामिति का ज्ञान ग्रीक यूनान पहुँचा । यूनानियों ने ज्यामिति का अर्थात बिन्दुओं , रेखाओं और समतल से बनी आकृतियों का अध्यन नापजोख अर्थात मेंसुरेशन ( Mensuration ) के माध्यम से किया । इन सम्बध में थेल्स ( 640 – 546 BC ) का स्थान प्रमुख है। थेल्स एक मिलेटस नगर का व्यापारी था । व्यापार के दौरान उसने बहुत धन अर्जित किया था । बाद की आयु उसने यात्रा और अध्ययन में बिताई। कहा जाता है कि मिश्र की यात्रा करते समय ज्यामिति में इसकी अभिरूचि पैदा हुई और यूनान लौटने पर उसने अपने मित्रों को जयामिति पढ़ाना आरंभ कर दिया । थेल्स के शिष्यों में सबसे अधिक प्रसिद्ध शिष्य हुए पाइथोगोरस लगभग ( 640 – 546 BC ) जिसका पाइथोगोरस प्रमेय बहुत प्रसिद्ध और महत्वपूर्ण है। ग्रीस का दूसरा अद्वितीय गणितज्ञ हुआ ‘ यूक्लिड ‘ जिसका जीवन काल 300 BC लगभग माना जाता है। इन्हें ज्यामिति का पिता कहा जाता है। कारण यह है कि उसने ज्यामिति के अध्ययन में विचार – विमर्श की एक नई परम्परा का सूत्रपात किया जिसमें कुछ मान्यताओं के आधार पर तर्कों के द्वारा प्रमाण दिया जाता है। इसने मान्यताओं और तर्कों पर आधारित ज्यामिति की एक पुस्तक निकाली जो तेरह खण्डों में विभक्त है। इस पुस्तक का नाम ‘ एलिमेन्टस ‘ है।
जहाँ एक ओर ज्यामिति के प्राचीन इतिहास के लिए मिश्र और बेबीलोनिया को याद किया जाता है तथा ज्यामिति के सुव्यवस्थित रूप से विस्तार के लिए ग्रीसवासियों की प्रशंसा की जाती है। वहाँ दूसरी ओर यह प्रमाण मिलता है कि प्राचीन भारत में भी ज्यामिति का अध्ययन किया गया था । ऐसा विश्वास किया जाता है कि पुराने जमाने में वैदिक अनुष्ठानों , जैसे यज्ञों आदि के लिए भिन्न – भिन्न प्रकार की वेदी के निर्माण में ज्यामिति का उपयोग होता था। मोहनजोदङो और हङप्पा की खुदाइयों से यह पता चलता है कि प्राचीन काल में ज्यामिति का उपयोग न केवल वेदियों की रचना में होता था , बल्कि सङक और मकान बनाने में भी इसका उपयोग होता था। तीन प्रसिद्ध भारतीय गणितज्ञों ने भी ज्यामिति के अध्ययन और विकास में अपना योगदान दिया है ।
1. भास्कर ( जन्म 114 BC) : जिन्होने पाइथोगोरस – प्रमेय का एक अतिरिक्त प्रमाण दिया ।
2. आर्यभट्ट ( जन्म 476 BC ) : जिन्होने किसी समद्विबाहु त्रिभुज के क्षेत्रफल , पिरामिड का आयतन , गोले का आयतन इत्यादि निकालने की प्रक्रियाएँ प्रस्तुत की ।
3. ब्रह्मपुत्र ( जन्म 598 AD ) : जिन्होंने किसी चक्रीय चतुर्भुज का क्षेत्रफल ज्ञात करने के लिये उनकी भुजाओं और अर्द्धपरिमिति वाला सूत्र बताया।
👉 ज्यामिति के अंग : ज्यामिति के निम्नलिखित अंग हैं।
(a). सैद्धान्तिक ज्यामिति ( Theoretical Geometry)
(b). प्रायोगिक ज्यामिति ( Practical Geometry )
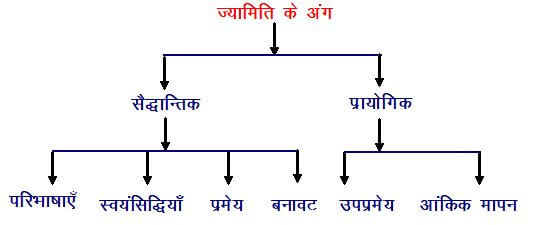
(a). सैद्धान्तिक ज्यामिति ( Theoretical Geometry)
ज्यामिति के उस अंग को, जिसमें प्रामाणित तथ्यों का परिचय, उपयोग एवं तर्क तथा स्वयंसिद्धियों की सहायता से नये नियमों के सत्यापन करने की व्यवस्था रहती है , सैद्धान्तिक ज्यामिति कहते हैं।
सैद्धान्तिक ज्यामिति के अंग :- सैद्धान्तिक ज्यामिति के प्रमुख अंग निम्नलिखित हैं।
(i). परिभाषाएँ :- ज्यामिति में व्यवहृत शब्दों एवं क्षेत्रों की परिभाषाएँ ।
(ii). स्वयंसिद्धियाँ :- वे ज्यामितिक सत्य जिन्हें प्रमाण के अभाव में भी स्वीकार कर लिया जाए , स्वयंसिद्धि कहलाती है।
(iii). प्रमेय :- ज्यामिति सम्बन्धी उन सत्यों को प्रमेय कहते हैं जिन्हें प्रामाणिक तथ्यों एवं तर्कों के द्वारा प्रमाणित किया जा सकता है।
(iv). उपप्रमेय : – प्रमाणित प्रमेयों की सहायता से किसी सिद्धांत के अभाव में भी सरलता से सिद्ध हो जाने वाले नियमों को उपप्रमेय कहते हैं।
(b). प्रायोगिक ज्यामिति (Practical Geometry )
ज्यामिति के जिस अंग में प्रामाणिक सिद्धान्तों की मदद से आकृतियों की रचना कर लेने का उपाय बताया गया हो तथा आंकिकमापन के द्वारा दो या दो से अधिक आकृतियों में सम्बन्ध स्थापित कर लेने की विधि सम्मिलित हो , उसे प्रायोगिक ज्यामिति कहते हैं।
प्रायोगिक ज्यामिति के अंग :- प्रायोगिक ज्यामिति के दो प्रमुख अंग हैं ।
(i). बनावट और (ii). आंकिक मापन
(i). बनावट: – इस अंग में दिए गए मापों के आधार पर विभिन्न चित्रों को उचित रूप में अंकीत कर लेने का ज्ञान मिलता है।
(ii). आंकिक मापन: – सैद्धांतिक ज्यामिति के द्वारा स्थापित आंकिक सम्बन्धों को सहारा लेकर एक की आकृति के बराबर या समरूप चित्रों को बना लेना या उसकी मापों का अध्ययन कर लेना , ज्यामिति के इसी अंग से संभव है।
👉 ज्यामिति के उपयोग
व्यावहारिक जीवन में असंख्य ऐसे काम हैं जिसे ज्यामिति की सहायता से सरलता पूर्वक पूरा किया जा सकता है।
उदाहरणस्वरूप : किसी घर का नक्सा बनाना , दो खेतों के क्षेत्रफलों की तुलना करना , एक चित्र के समरूप दूसरा चित्र खींचना , इत्यादि काम ऐसे हैं जो कल्पना या अन्दाज से कठिन से प्रतीत होते हैं पर ज्यामिति उसे आसानी से कर डालती है। इतना ही नहीं पानी की धारा का वेग , पहाङ की ऊँचाई , सङक निर्माण करना , घर में बिजली का तार लगाना इत्यादि समस्याओं को भी ज्यामिति आसानी से सुलझा लेती है।
1. रेखा गणित (Geometry ) :- रेखा गणित वह गणित है जिसमें समतल ठोस, रेखा के गुणों तथा बनावट का वर्णन रहता है।
2. बिंदु ( Point ) :- बिंदु एक ऐसी ज्यामितिय आकृति है जो अपरिभाषित है ।
या बिन्दु वह ज्यामितिय आकृति है जिसका स्थान तो नियत होता है लेकिन लम्बाई , चैङाई और मोटाई नियत नहीं होती है।
व्यावहारिक रूप में परिभाषा के आधार पर बिन्दु का उदाहरण प्राप्त करना असम्भव है क्योंकि बारिक पेंसिल की नोक का चिहृ भी कुछ – न – कुछ परिमाण रखता ही है ।
अत: बिन्दु वह ज्यामितीय आकृति है जो कम से कम स्थान को घेरता हो ।

चिहृ A , B , C और D में से प्रत्येक बिन्दु है, पर बिन्दु D की तुलना में प्रथम तीन अशुद्ध है । बिन्दु D यथासम्भव छोटा है और यही शुद्ध भी है।
3. रेखा (Line ) :- रेखा वह ज्यामितिय आकृति है जो बिंदुओं से मिलकर बनी होती है । रेखा का लंबाई तो नियत होता है लेकिन मोटीई नियत नहीं होता है।
![]()
रेखा के प्रकार : – रेखाएँ दो प्रकार की होती है।
(i). सरल रेखा (Straight Line ) और (ii). वक्र रेखा (Curved Line )
(i). सरल रेखा (Straight Line ) :- वह रेखा जिसकी दिशा नहीं बदलती , सरल रेखा कहलाती है ।
![]()
(ii) वक्र रेखा (Curved Line ) :- वह रेखा जिसकी दिशा बदलती है, वक्र रेखा कहलाती है ।
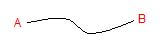
4. समांतर रेखाएँ (Parallel Lines ) :- एक ही तल में स्थित दो या दो से अधिक रेखाएं जिसके बीच के लंबवत दूरी हमेशा समान हो तथा अनंत बिंदु तक वे रेखाएँ एक दूसरे को प्रतिच्छेदित नहीं करती हो समांतर रेखाएं कहलाती है।
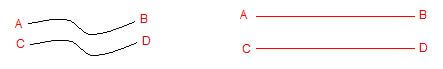
5. संगामी रेखाएँ (Concurrent Lines) :- दो या दो से अधिक वैसी रेखाएं जो एक ही बिंदु पर प्रतिच्छेदित करती हो, उसे संगमी रेखाएं कहते हैं तथा जिस बिंदु पर प्रतिच्छेदित करती है उसे संगमी बिंदु कहते हैं ।
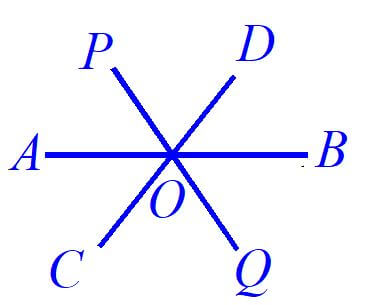
रेखा AB, CD तथा PQ संगामी रेखा तथा O संगमी बिंदु हैं।
6. प्रतिच्छेद बिंदु (Intersection Point) :- जिस बिंदु पर दो या दो से अधिक रेखाएं प्रतिच्छेद करती है उस बिंदु को प्रतिच्छेदित बिंदु कहते हैं ।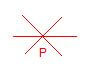
P प्रतिच्छेद बिंदु है।
7. तिर्यक रेखा (Tranversal Lines) :- वह रेखा जो दो या दो से अधिक रेखाओं को काटे , तिर्यक रेखा कहलाती है ।
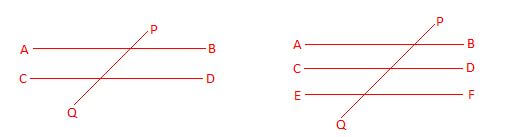
PQ तिर्यक रेखा है ।
8. किरण (Ray) :- जिस रेखा के एक छोर को अनन्त तक बढाया जाय किन्तु दूसरी छोर को सीमित बिन्दु तक रखा जाय , किरण कहलाती है।

9. रेखाखण्ड (Line Segment ):- किसी रेखा पर दो बिंदुओं द्वारा घिरे बिच के खण्ड को रेखाखण्ड कहते है।

10. क्षैतिज रेखा Horizontal Line ) :- जो रेखा पृथ्वी सतह के समांतर हो, उसे क्षैतिज रेखा कहते हैं।

11. उदग्र रेखा (Vertical Line ) :- जो रेखा पृथ्वी सतह के लंबवत हो उसे उदग्र रेखा कहते हैं।

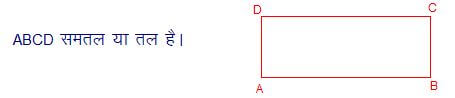
12. समतल या तल (Plane ) :- जिस सतह का लंबाई एवं चौड़ाई हो लेकिन मोटाई न हो उस सतह को समतल सतह कहते है।
13. ठोस (Solid ) :- जिस वस्तु में लंबाई चौड़ाई तथा मोटी तीनों हो उसे ठोस कहते हैं ।
जैसे – दियासलाई , ईंट , साबुन इत्यादि ।

14. कोण (Angle ) :– किसी रेखाखंड पर जब कोई दूसरा रेखाखंड आकर मिलती है तो इस प्रकार दोनों रेखाखण्डों के बीच जो झुकाव उत्पन्न होता है उसे कोण कहते हैं । इसे ∠ द्वारा सूचित किया जाता है।
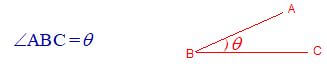
कोण के प्रकार (Types of Angle)
| माप के आधार पर | बनावट के आधार पर |
| न्यून कोण (Acute Angle) | आसन्न कोण (Adjacent Angle) |
| समकोण (Right Angle ) | सम्मुख कोण (Vertical opposite Angle) |
| अधिक कोण ((Obtuse Angle) | अन्तः कोण (Interior Angle) |
| ऋजु कोण (Straight Angle) | बहिष्कोण (Exterior Angle) |
| पुनर्युक्त कोण (Reflex Angle) | एकान्तर कोण (Alternate Angle) |
| अनुपूरक कोण (Complementary Angle) | संगत कोण (corresponding Angle) |
| सम्पूरक कोण (Supplementary Angle) |
माप के आधार पर : –
(i). न्यून कोण (Acute Angle) :– जिस कोण की माप 00 से बड़ा तथा 900 से छोटा हो, उसे न्यून कोण कहते हैं।

(ii). समकोण (Right Angle ) :- जिस कोण की माप 900 के बराबर हो, उसे समकोण कहते हैं ।

(iii). अधिक कोण ( Obtuse Angle ) :- जिस कोण की माप 900 से बड़ा तथा 1800 से छोटा हो, उसे अधिक कोण कहते हैं ।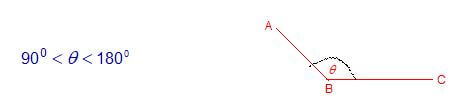
(iv). ऋजु कोण या रेखीय कोण ( Straight Angle ) :- जिस कोण की माप 1800 डिग्री के बराबर हो, उसे ऋजु कोण या रेखीय कोण कहते हैं ।
(v). वृहत् कोण या पुनर्युक्त कोण ( Reflex Angle ) :- जिस कोण की माप 1800 से बड़ा तथा 3600 से छोटा हो, उसे वृहत् कोण या पुनर्युक्त कोण कहते हैं ।

(vi). पूरक कोण या कोटीपूरक कोण ( Complementary Angle ) :- किसी बिन्दु पर बने दो कोणों का योग 900 या एक समकोण के बराबर हो, तो वे दोनों कोण एक दूसरे का पूरक कोण या कोटीपूरक कोण कहलाती है। 
(vii). सम्पूरक कोण ( Supplementary Angle ) :- किसी बिन्दु पर बने दो कोणों का योग 1800 या दो समकोण के बराबर हो, तो वे दोनों कोण एक दूसरे का सम्पूरक कोण कहलाती है।

बनावट के आधार पर –
(i). आसन्न कोण ( Adjacent Angle ) :- किसी उभयनिष्ट सरल रेखा के दोनों ओर बने कोणों को आसन्न कोण कहते हैं।

(ii). सम्मुख कोण या शीर्षाभिमुख कोण ( Vertical Opposite Angle ) :- जब दो सरल रेखाएँ किसी बिन्दु पर एक-दूसरे को काटती है तो बने आमने-सामने के कोणों को सम्मुख कोण या शीर्षाभिमुख कोण कहते हैं।
अर्थात 
(iii). अन्तः कोण ( Interior Angle ) :- दो से अधिक सरल रेखाओं द्वारा घिरे हुए क्षेत्र के अन्दर का कोण अन्तः कोण कहलाता हैं।
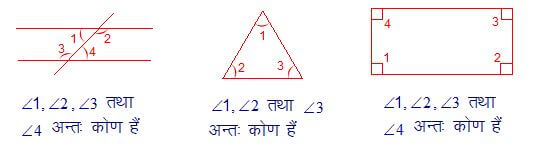
(iv). बहिष्कोण ( Exterior Angle ) :- किन्हीं दो सरल रेखाओं को अगर तीसरी रेखा काटती हो अथवा कोई क्षेत्र दो से अधिक सरल रेखाओं से घिरी हो और उसकी किसी भुजा को बढ़ा दी जाए तो बाहर के सभी कोण बहिष्कोण कहलाते हैं।

(v). एकान्तर कोण ( Alternate Angle ) :- दो रेखाओं या दो समांतर रेखाओं को यदि तीसरी सरल रेखा, काटती है, तो दोनों रेखाओं से घिरे वे दोनों कोण एकान्तर कोण कहलाते हैं जो तीसरी सरल रेखा के दोनों ओर एक – एक करके एकान्तर क्रम में ऊपर – नीचे होती है।

(vi). संगत कोण ( Corresponding Angle ) :- दो रेखाओं या दो समांतर रेखाओं को यदि तीसरी सरल रेखा, काटे तो तीसरी सरल रेखा के एक ही ओर के एक अन्तःकोण और उसके सामने के बहिष्कोण को संगत कोण कहलाती है।


| भुजाओं के आधार पर | कोण के आधार पर |
| विषमबाहु त्रिभुज ( Scalene Triangle ) | न्यूनकोण त्रिभुज ( Acute Angle Triangle ) |
| समद्विबाहु त्रिभुज ( Isosceles Triangle) | समकोण त्रिभुज ( Right Angle Triangle ) |
| समबाहु त्रिभुज ( Equilateral Triangle ) |
अधिककोण त्रिभुज ( Obtuse Angle Triangle )
|
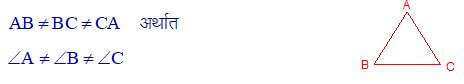


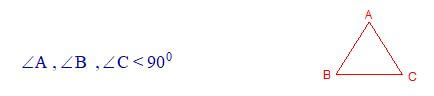









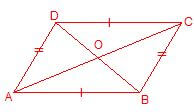
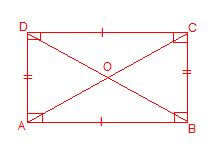
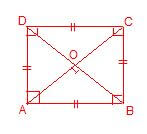
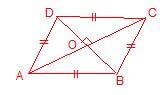
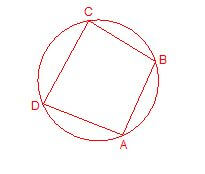
24. बहुभुज ( Polygon ) :- वह समतल क्षेत्र जो चार से अधिक भुजाओं से घिरा हो बहुभुज कहलाती है ।
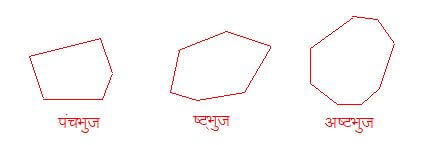
25. समबहुभुज ( Regular Polygon ) :- जिस बहुभुज के सभी भुजाएं आपस में बराबर हो, उसे समबहुभुज कहते हैं । समबहुभुज के सभी कोण आपस में बराबर होती है।