1. Vector : Which physical quantity has magnitude and direction are called vector quantities.
Example : Displacement , Velocity , Acceleration , Force…………………..etc.
2. Characterisation of a Vector :
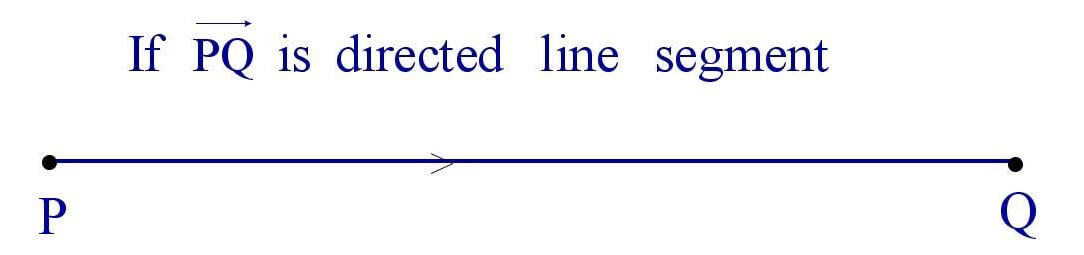
(i). Length :

(ii). Support :

(iii). Sense :

(iv). Notation of a Vector :

3. Representation of a Vector :

4. Types of Vectors :
(i). Zero Vector or Null Vector :

(ii). Proper Vector :

(iii). Unit Vector :

Note :

(iv). Parallel Vectors :

(v ). Like and Unlike Vectors :

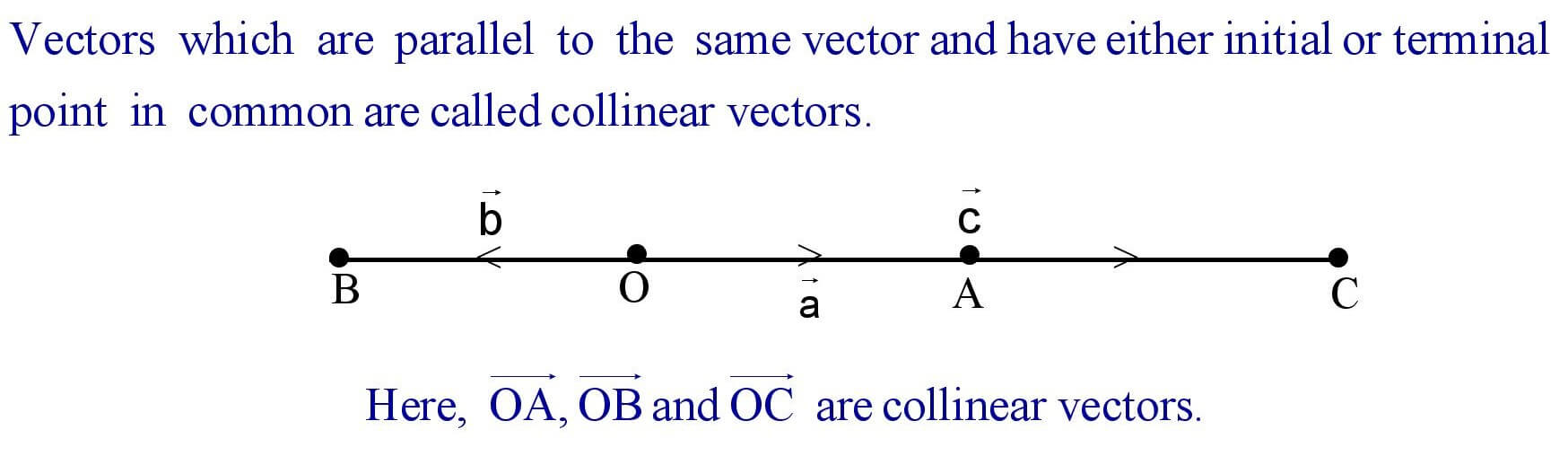
(vi). Collinear Vectors :
(vii). Non – collinear Vectors :

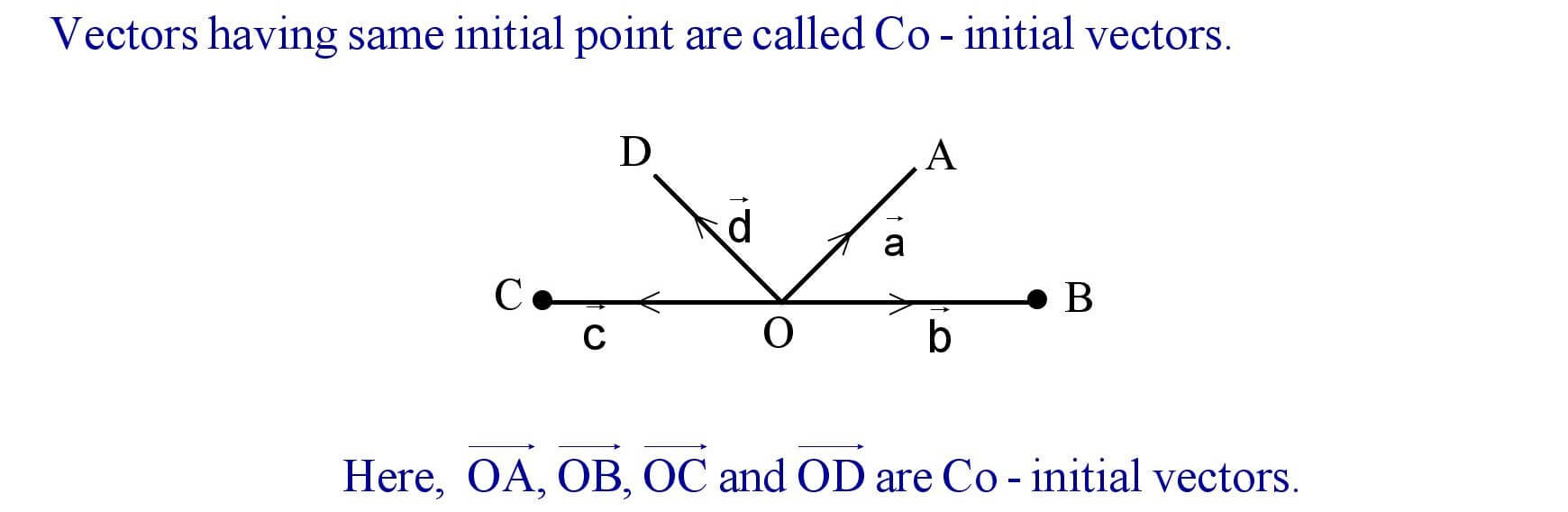
(viii). Co – initial vectors :
(ix). Free Vectors :

(x). Equal Vector : 
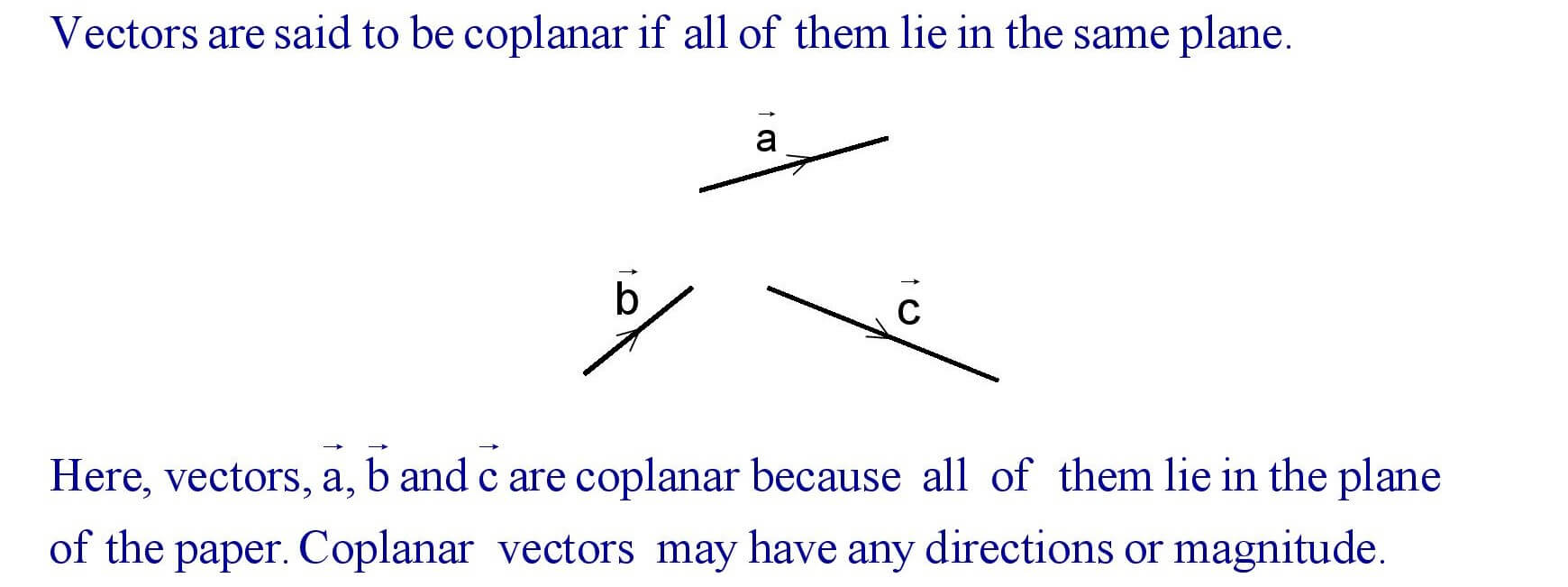
(xi). Coplanar Vector :
(xii). Localised Vectors :

(xiii). Reciprocal Vectors :

5. Position Vector of a Point :

6. Addition of two Vectors :

7. Triangle law of addition :

8. Parallelogram law of addition :

9. Addition in component form :

10. Properties of Vector addition : Vector addition has the following properties.
(i). Binary operation :

(ii). Commutativity :
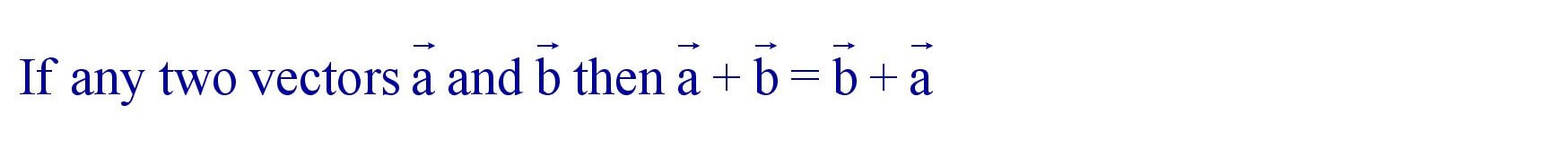
(iii). Associativity :
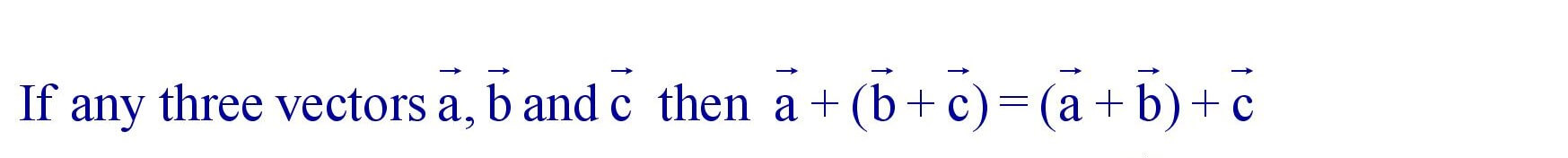
(iv). Identity :
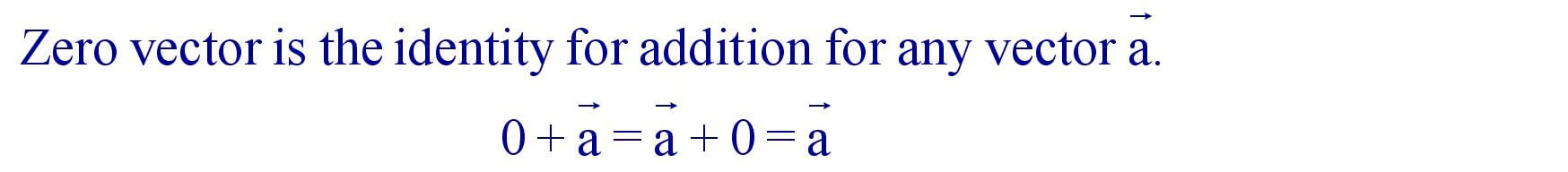
(v). Additive Inverse :
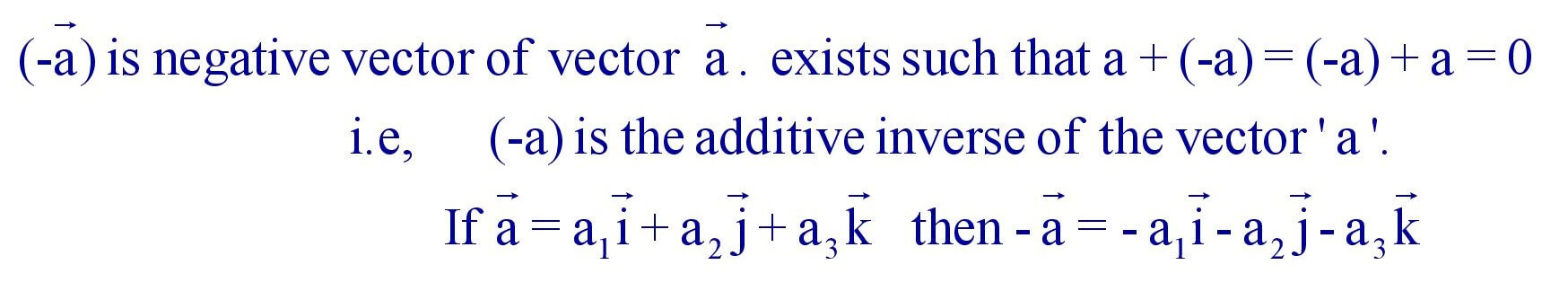
(vi). Cancellation law :

11. Subtraction of Vectors :

Example :
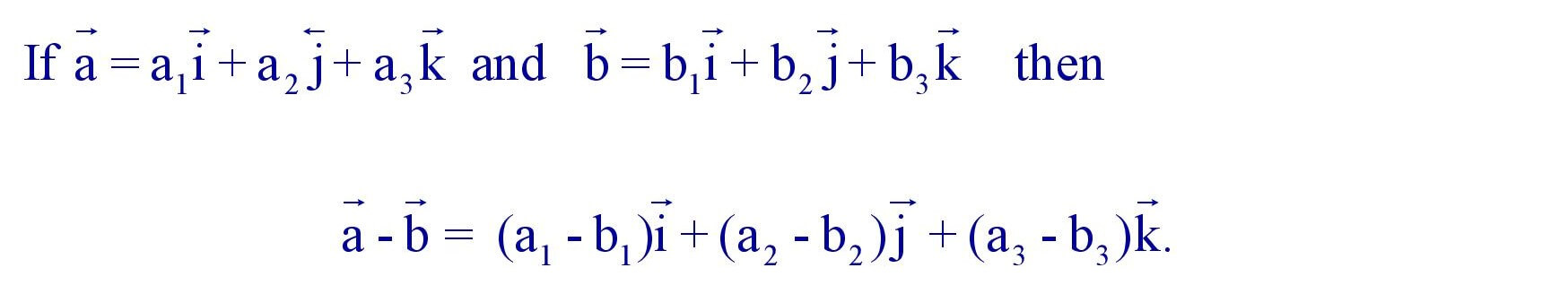
Note :

12. Vectors in terms of position vectors of end points :
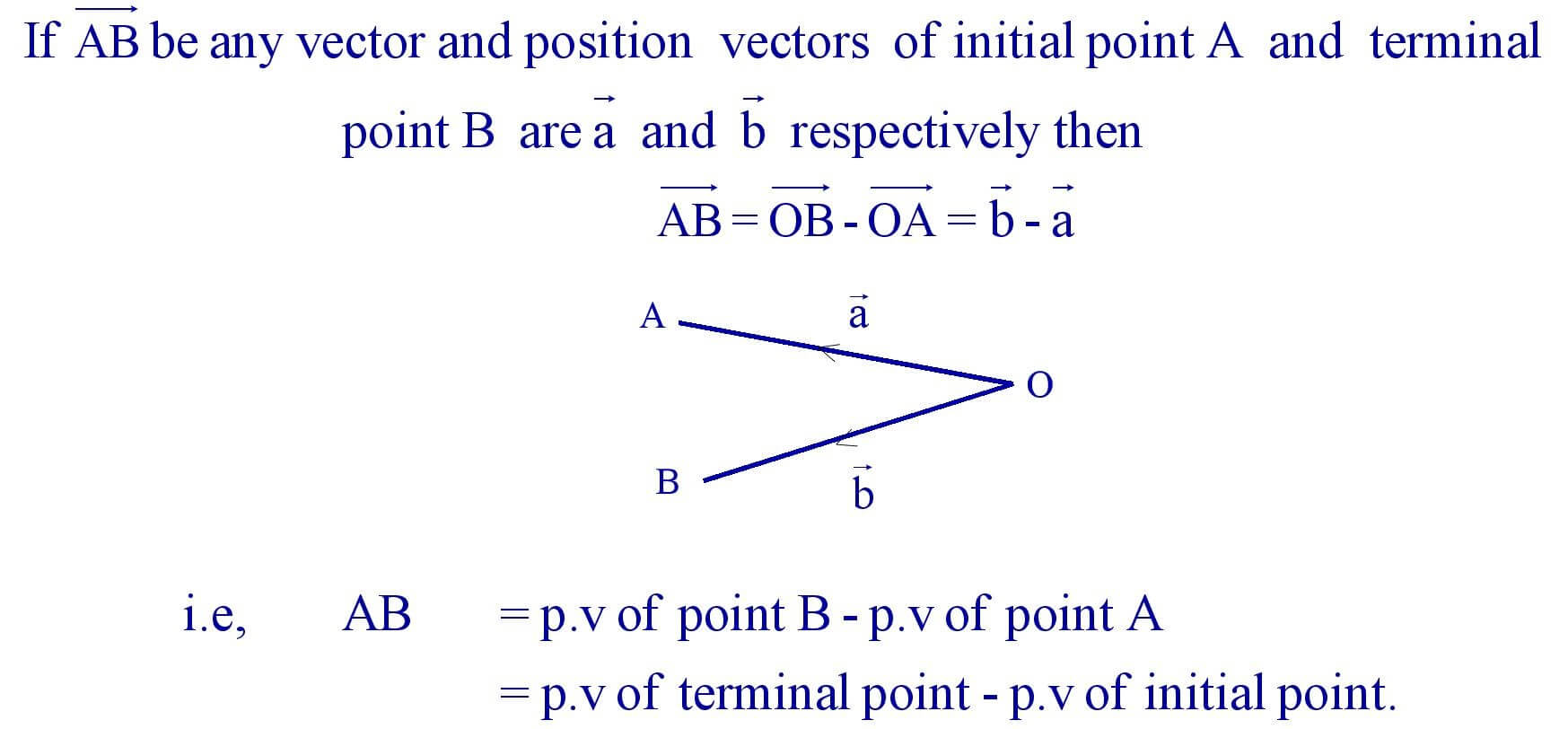
13. Multiplication of a vector by a scalar :

Example :
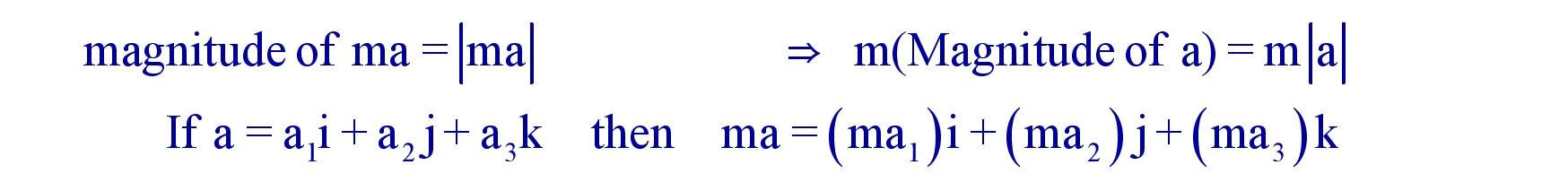
Note :

Properties Multiplication of a vector by a scalar :

14. Modulus of a Vector :

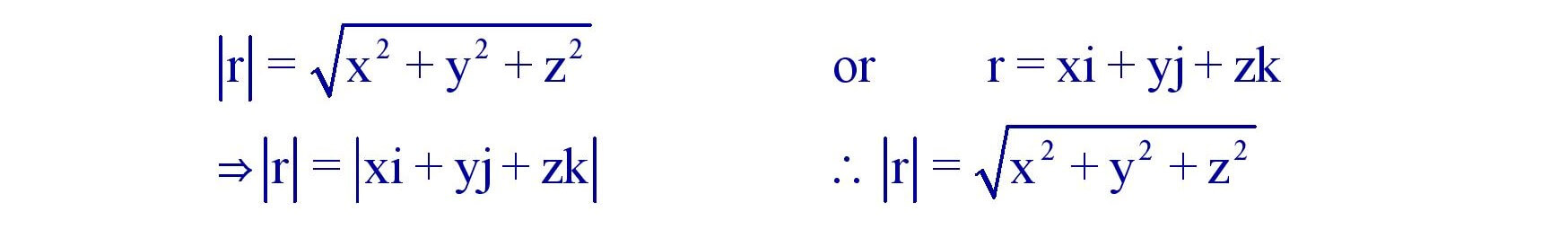
15. Collinearity of three Points :

16. Relation between two parallel and perpendicular vectors :


17. Direction Cosines of a vector :

18. Co-planar and non – co-planar vectors : Vectors are said to be co-planar if they lie in the same plane or they are parallel to the same plane otherwise they are said to be non – co-planar.

19. Components of a vector in two Dimensions :

20. Components of a vector in three Dimensions :

21. The equation of a straight line :

22. Disector of the angle between two straight lines.
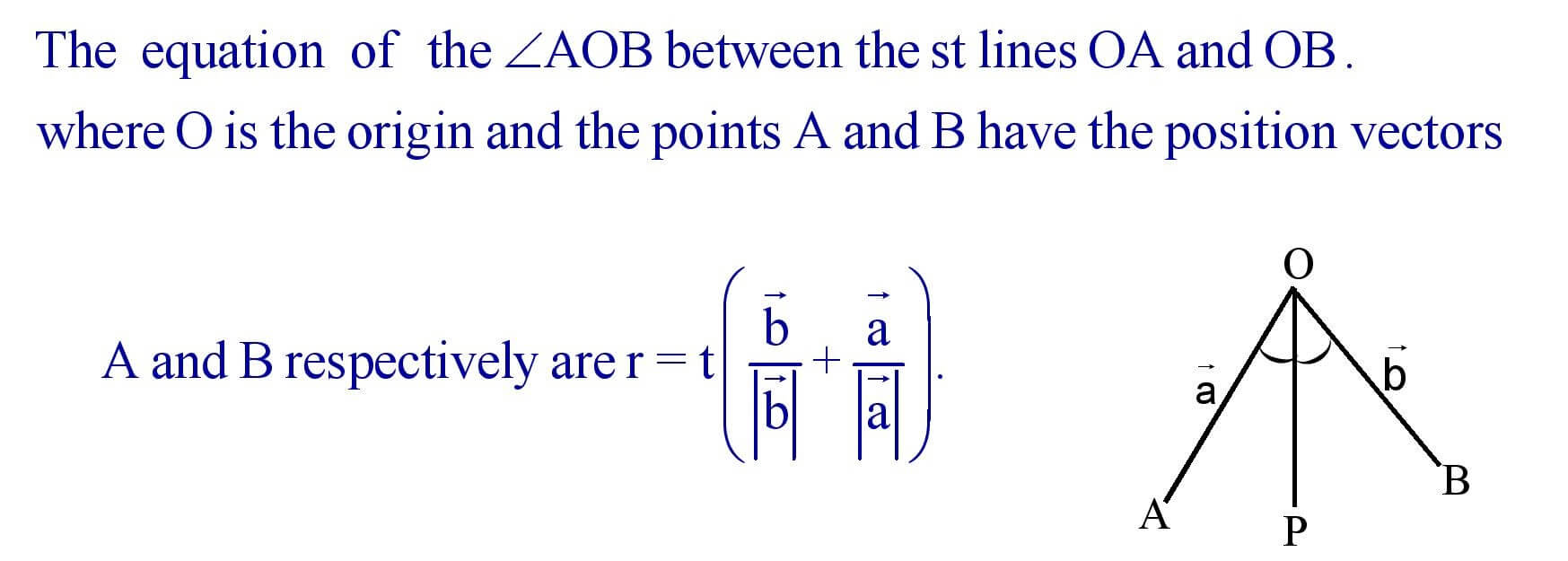
23. Equation of a plane :

Note :

24. Ceva’s Theorem :

25. Menelau’s Theorem :

26. Centroid :

27. Section Formula :
(i). Internal Division :
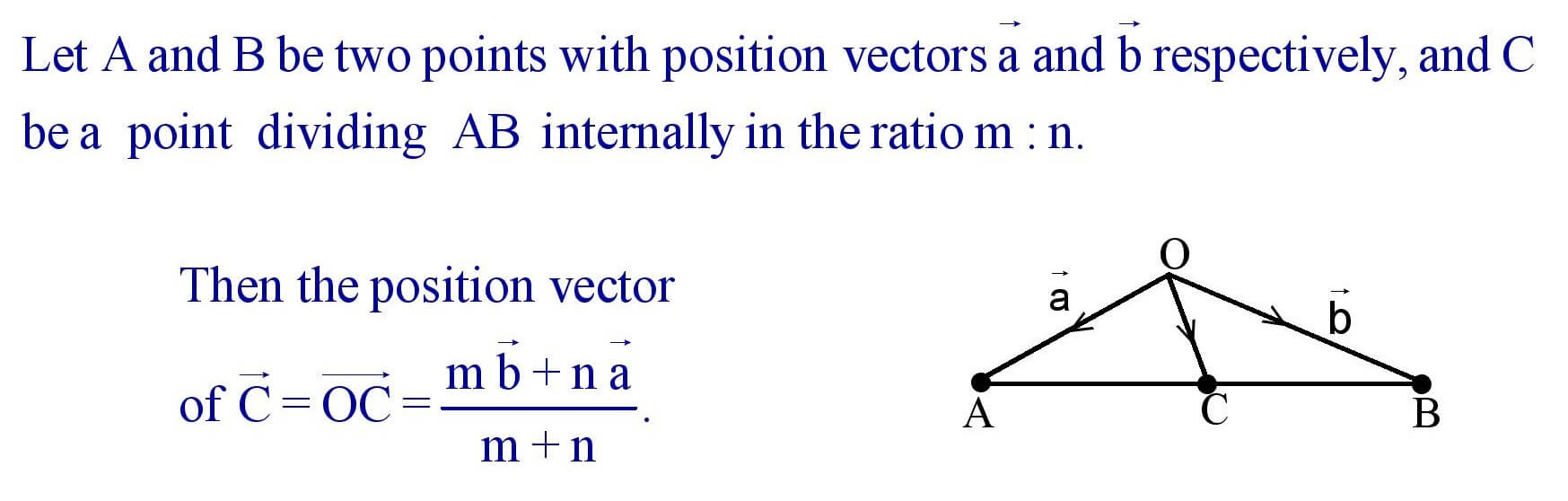
(ii). External Division :

(iii). Centroid of Triangle :
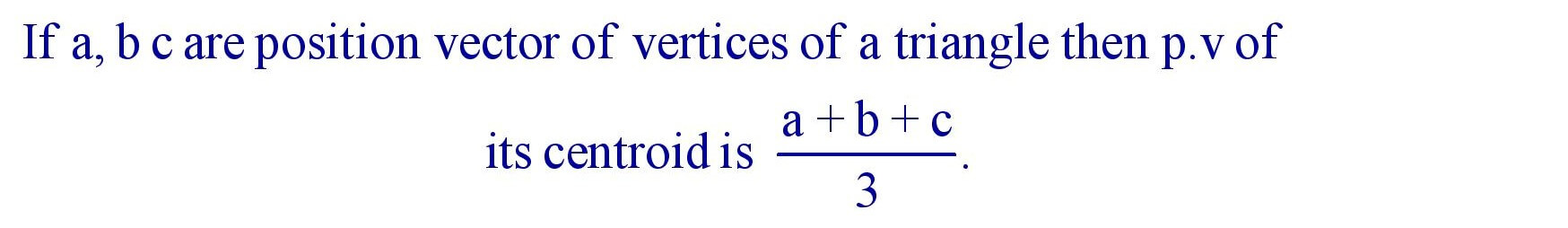
| Click Here to pdf download |

