How to Proof Compound Angle Formula

Compound Angle Formula : Algebraic sum of two or more angles is called compound angle.

If A, B and C are any angle then A + B , A + B + C, A – B + C, A + B – C, A – B – C, A – B ………..etc are all compound angles.

Addition of Compound Angle Formula : 

1. Sin (A + B) = SinA.CosB + CosA.SinB
2. Sin (A + B) = SinA.CosB + CosA.SinB
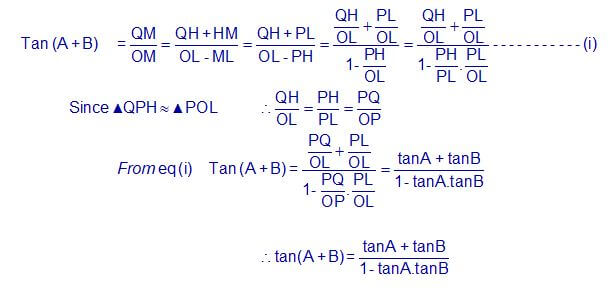
3. Tan (A + B) = TanA + TanB/ 1 – TanA.TanB

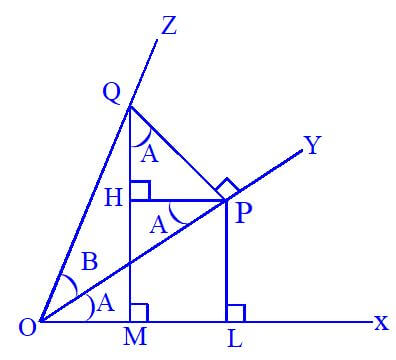
Let the revolving line starting from the position ox with angle A and again revolving in same direction with angle B.

∴  ∠ Xoy = A  and ∠Xoy = B  then ∠XOZ = A + B                                 Let Q be a any point on oz.

Draw QM ⊥ OX   and QP ⊥ OY from point Q.    Draw PH ⊥ QM from Point P

Now  ∠HPO  =   ∠POX =  A                            ∴ ∠HPO = 90^o

∠ HPO  = 90^o – A                                             ∴ ∠HQP = A

In Δ QOM 

Subtraction of Compound Angle Formula : 

1. Sin (A – B) = SinA.CosB – CosA.SinB
2. Sin (A – B) = SinA.CosB – CosA.SinB
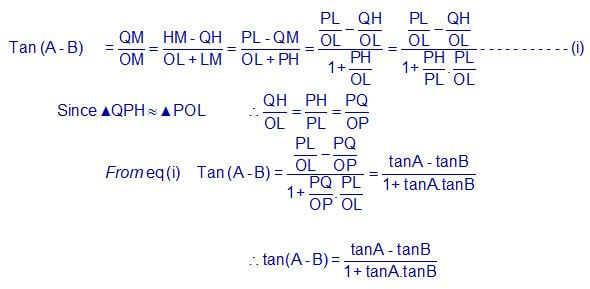
3. Tan (A – B) = TanA – TanB/ 1 + TanA.TanB

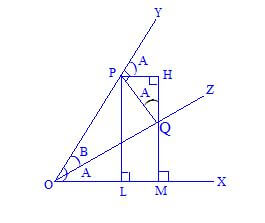
Let the revolving line starting from the position ox with angle A and again revolving in opposite direction with angle B.

∴  ∠ Xoy = A  and ∠Xoy = B  then ∠XOZ = A – B                                 Let Q be a any point on oz.

Draw QM ⊥ OX   and QP ⊥ OY from point Q.    Draw PH ⊥ QM from Point P.

Now  ∠YPH  =   ∠POX =  A                            ∴ ∠QPY = 90^o

∠ QPH  = 90^o – A                                             ∴ ∠HQP = A

In Δ QOM 

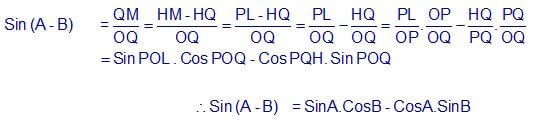
Compound Angle Formula :