सिद्धांत संख्या – 1
यदि दो कोणों की मापों का योग 1800 हो तो उसे संपूरक कोण कहते हैं।

सिद्धांत संख्या – 2
यदि दो कोणों की मापों का योग 900 हो तो उसे पूरक कोण कहते हैं ।
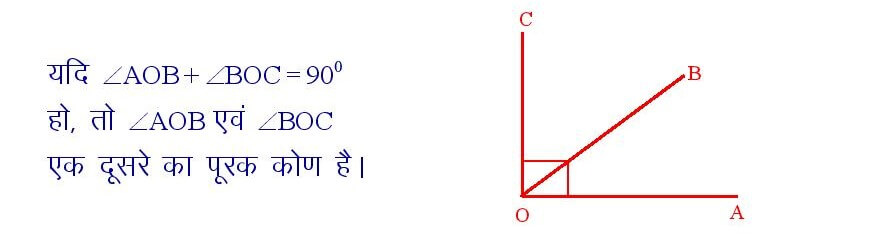
सिद्धांत संख्या – 3
यदि कोई किरण किसी रेखा पर आधारित हो, तो इस प्रकार बने दो आसन्न कोणों का योग 1800 होता है ।
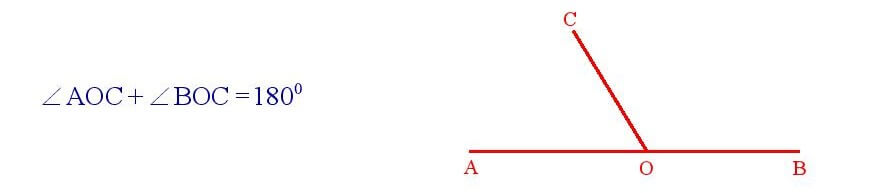
सिद्धांत संख्या – 4
यदि दो आसन्न कोणों का योग 1800 हो , तो उनकी बाह्म भुजाएँ एक ही रेखा में होती है।

सिद्धांत संख्या – 5
यदि दो रेखाएं परस्पर काटती हो , तो शीर्षाभिमुख कोण समान होती है।
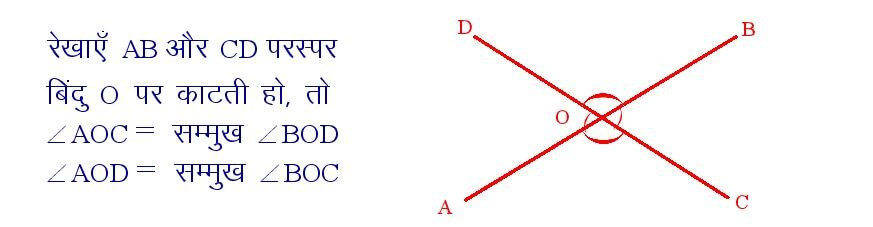
सिद्धांत संख्या – 6
यदि कोई तिर्यकछेदी रेखा दो समानांतर रेखाओं को प्रतिच्छेद करती है , तो संगत कोणों का युग्म समान होता है।

सिद्धांत संख्या – 7
यदि कोई तिर्यकछेदी रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करें कि संगत कोणों का युग्म समान हो, तो रेखाएं समानांतर होती है।
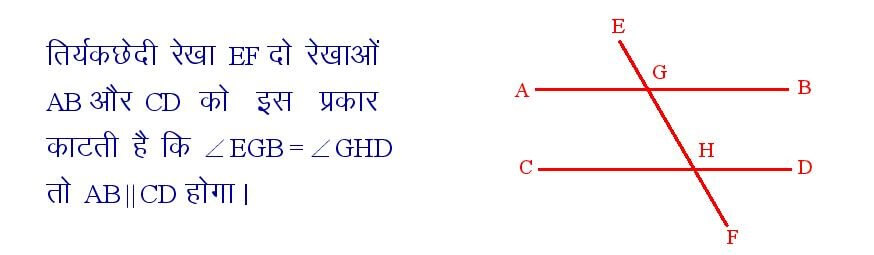
सिद्धांत संख्या – 8
यदि कोई तिर्यकछेदी रेखा दो समानांतर रेखाओं को प्रतिच्छेद करती है तो –
(a). एकांतर कोणों का प्रत्येक युग्म समान होता है।
(b). तिर्यकछेदी रेखा के एकही ओर के अंतः कोणों का योग 1800 होता है।

सिद्धांत संख्या – 9
यदि कोई तिर्यकछेदी रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करें कि एकांतर कोण समान हो तथा तिर्यकछेदी रेखा के एक ही ओर के दो अंतः कोणों का योग संपूरक हो , तो रेखाएं समानांतर होती है।

सिद्धांत संख्या – 10
रेखाएं जो किसी अन्य रेखा के समानांतर होती है आपस में भी समानांतर होती है।

सिद्धांत संख्या – 11
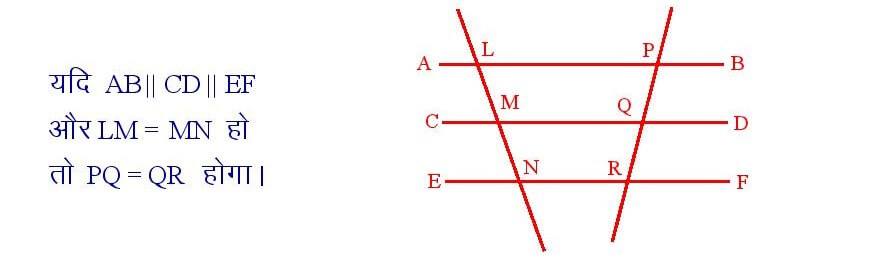
यदि कोई तिर्यकछेदी रेखा तीन समानांतर रेखाओं द्वारा बनाए गए अंतः खंड यदि बराबर हो, तो किसी भी अन्य तिर्यकछेदी रेखा पर बनाए गए तदनुरूपी अंतःखंड भी बराबर होंगे ।
सिद्धांत संख्या – 12
दो प्रतिच्छेदी रेखाओं से समदूरस्थ किसी बिंदु का बिंदुपथ उस नियत रेखाओं द्वारा बने कोणों के समद्विभाजकों का एक युग्म होता है।
